Outline
Topics
- Review of basic probability theory concepts: outcome, event, sample space
- Intuition from the Bayesian perspective
Rationale
- One definition of Bayesian inference: applying probability theory to statistical inference problems
- Therefore, it is critical to understand probability to learn Bayesian inference
- This week, we will help you “reload in memory” some of the most important bits of probability theory used in this course
Definitions
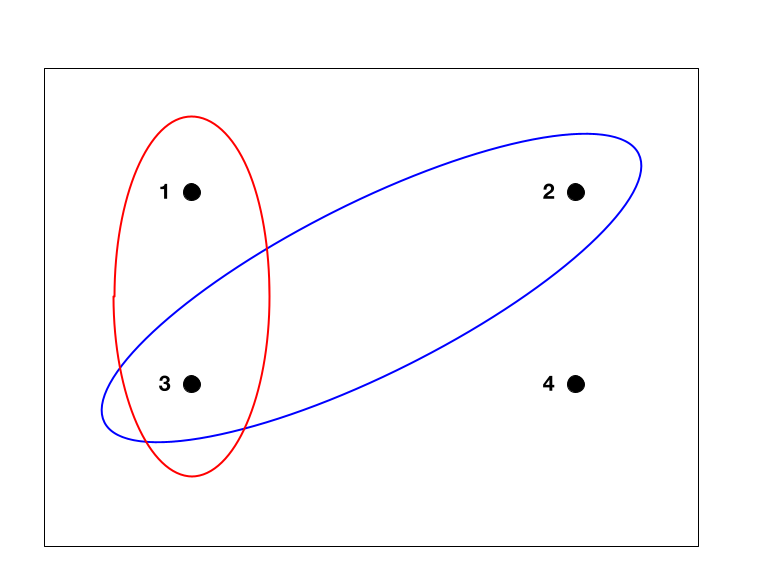
- Sample space, denoted \(S\), a set.
- Example: \(S = \{1, 2, 3, 4\}\) (see Figure).
- Each element \(s\) of \(S\) is called an outcome, \(s \in S\).
- Example: each of the 4 points.
- A set of outcomes \(E \subset S\) is called an event.
- Example: \(E = \{s \in S : s \text{ is odd}\}\) (red in the Figure).
Intuition: Bayesian view
- In Bayesian statistics, an outcome will describe the state of the world.
- We do not know which outcome is the true state of the world.
- We observe partial information on the state of the world/outcome.
- We rule out the outcomes that are not consistent with the observation…
- …but there will be several outcomes left!
- We will deal with this situation using probability theory.
Intuition: randomized algorithms
- An algorithm is “randomized” if it has access to virtual dices/coins.
- In practice this is done using pseudorandom number generators.
- In this context an outcome is a random seed, i.e. the initialization of the pseudorandom number generator.