Grouped data

Outline

Topics

• Using the package tidybayes to feed complex data into Stan.

Rationale

Data organized in various groups is a frequent feature of Bayesian models, in particular in hierarchical models.

Getting grouped data into stan is tedious and error prone. The package tidybayes automates much of this.

Pre-reading

If you have never heard about “tidy data”, while it is not strictly essential for this course, it is a good investment to skim this tutorial on tidy data.

Example

First, install the packages magrittr and tidybayes (and ggplot2 if you have not done so already), then import them:

suppressPackageStartupMessages(require(rstan))
suppressPackageStartupMessages(require(magrittr))
suppressPackageStartupMessages(require(tidybayes))
suppressPackageStartupMessages(require(ggplot2))

Data prep

We load the data used in exercise 6:

data = read.csv(url("https://raw.githubusercontent.com/UBC-Stat-ML/web447/main/exercises/ex06_assets/vaccines_full.csv"))
data$is_vaccinated = ifelse(data$arms == "vaccinated", 1, 0)
rmarkdown::paged_table(data)

The magic conversion of “tidy data” (data in a format like the above) into a format that can be consumed by Stan is done using compose_data:

stan_converted = compose_data(data)

stan_converted

$trials
[1] 1 1 3 3 2 2

$n_trials
[1] 3

$arms
[1] 2 1 2 1 2 1

$n_arms
[1] 2

$groupSizes
[1]  5807  5829 18198 18325 14134 14073

$numbersOfCases
[1]  30 101   8 162  11 185

$is_vaccinated
[1] 1 0 1 0 1 0

$n
[1] 6

Stan model

Here we consider a simple, non-hierarchical model but fitting all the data at once. In the exercise, you will modify this model to follow the hierarchical structure of exercise 6.

data {
  int n;
  int n_trials;
  array[n] int<lower=1,upper=n_trials> trials;
  array[n] int arms;
  int n_arms;
  array[n] int groupSizes;
  array[n] int numbersOfCases;
  array[n] int is_vaccinated;
}

parameters {
  vector<lower=0,upper=1>[n_trials] efficiencies;
  vector<lower=0,upper=1>[n_trials] prevalences;
}

model {

  for (trial in 1:n_trials) {
    efficiencies[trial] ~ beta(1, 1);
    prevalences[trial] ~ beta(1, 1);
  }

  for (i in 1:n) {
    numbersOfCases[i] ~ binomial(groupSizes[i], prevalences[trials[i]] * (is_vaccinated[i] == 1 ? 1.0 - efficiencies[trials[i]] : 1.0));
  }
}

Fitting

The fit object returned by sampling does not know about the string labels attached to each trial integer index. We use fit %<>% recover_types(data) to add back that information:

fit = sampling(
  vaccines,
  seed = 1,
  data = stan_converted, 
  refresh = 0,
  iter = 10000                  
)
fit %<>% recover_types(data)

Getting draws

The output of Stan is not tidy either.

fit

Inference for Stan model: anon_model.
4 chains, each with iter=10000; warmup=5000; thin=1; 
post-warmup draws per chain=5000, total post-warmup draws=20000.

                    mean se_mean   sd     2.5%      25%      50%      75%
efficiencies[1]     0.69    0.00 0.07     0.55     0.65     0.69     0.73
efficiencies[2]     0.94    0.00 0.02     0.89     0.92     0.94     0.95
efficiencies[3]     0.94    0.00 0.02     0.90     0.93     0.95     0.96
prevalences[1]      0.02    0.00 0.00     0.01     0.02     0.02     0.02
prevalences[2]      0.01    0.00 0.00     0.01     0.01     0.01     0.01
prevalences[3]      0.01    0.00 0.00     0.01     0.01     0.01     0.01
lp__            -2793.24    0.02 1.77 -2797.52 -2794.21 -2792.89 -2791.93
                   97.5% n_eff Rhat
efficiencies[1]     0.80 22048    1
efficiencies[2]     0.97 23668    1
efficiencies[3]     0.97 24974    1
prevalences[1]      0.02 22889    1
prevalences[2]      0.02 25768    1
prevalences[3]      0.01 25400    1
lp__            -2790.81  8951    1

Samples were drawn using NUTS(diag_e) at Thu Mar 14 17:33:47 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

Use spread_draws to put the draws into a tidy format:

fit %>% spread_draws(efficiencies[trials], prevalences[trials]) %>% head(10)

# A tibble: 10 × 6
# Groups:   trials [1]
   trials               efficiencies .chain .iteration .draw prevalences
   <chr>                       <dbl>  <int>      <int> <int>       <dbl>
 1 AZ-Oxford (combined)        0.479      1          1     1      0.0120
 2 AZ-Oxford (combined)        0.862      1          2     2      0.0218
 3 AZ-Oxford (combined)        0.712      1          3     3      0.0194
 4 AZ-Oxford (combined)        0.695      1          4     4      0.0163
 5 AZ-Oxford (combined)        0.660      1          5     5      0.0164
 6 AZ-Oxford (combined)        0.642      1          6     6      0.0188
 7 AZ-Oxford (combined)        0.613      1          7     7      0.0176
 8 AZ-Oxford (combined)        0.720      1          8     8      0.0150
 9 AZ-Oxford (combined)        0.645      1          9     9      0.0150
10 AZ-Oxford (combined)        0.687      1         10    10      0.0164

Plotting

Now that we have draws in tidy format, instead of using specialized MCMC plotting libraries we can just use ggplot:

fit %>%
  spread_draws(efficiencies[trials]) %>%
  ggplot(aes(x = efficiencies, y = trials)) +
  stat_halfeye() + 
  theme_minimal()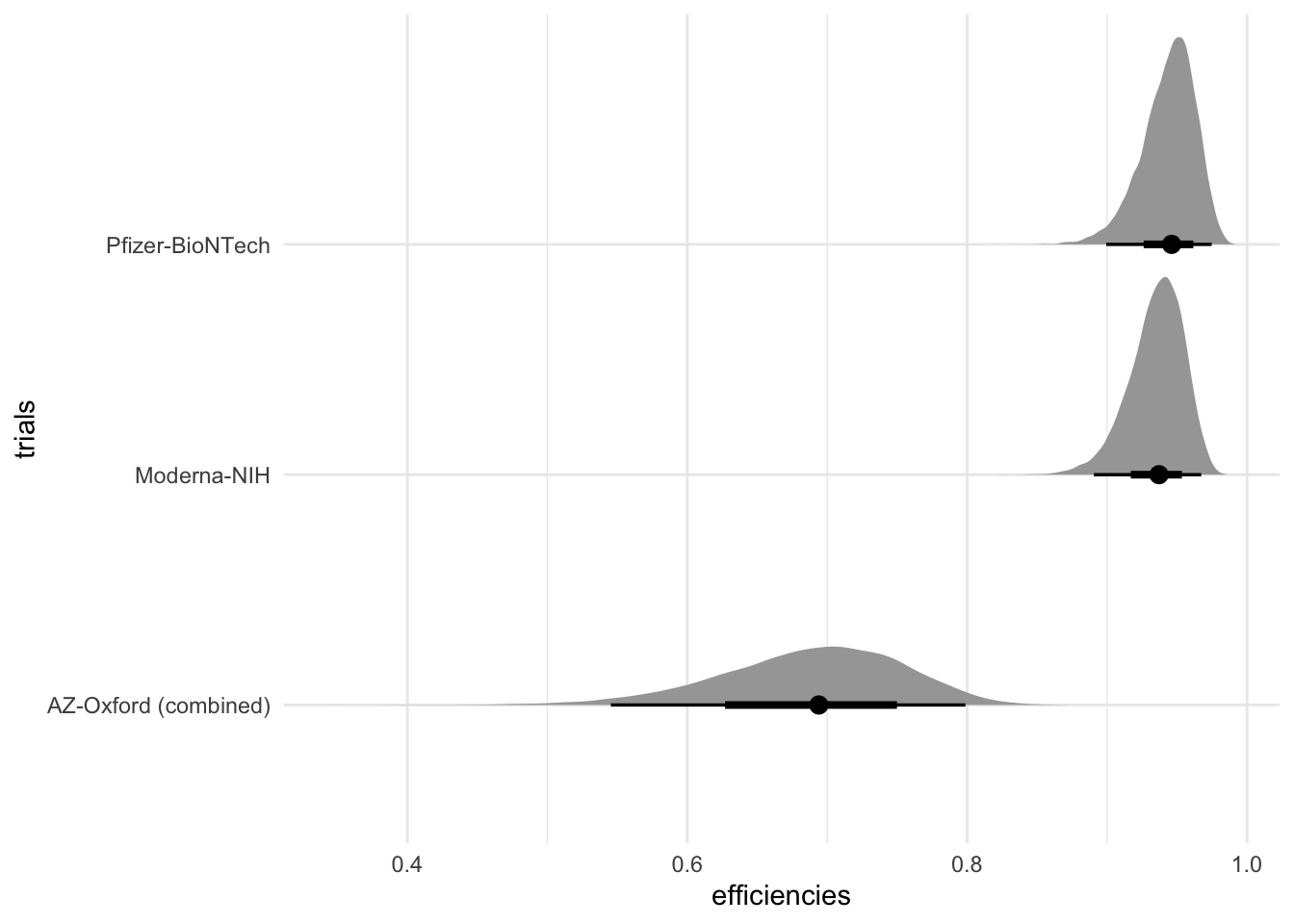

This makes it easier to customize plots.

Summaries

tidybayes also offers convenient ways to compute summaries such as High Density Intervals (HDI)

fit %>%
  spread_draws(efficiencies[trials]) %>%
  median_hdi(efficiencies)

# A tibble: 3 × 7
  trials               efficiencies .lower .upper .width .point .interval
  <chr>                       <dbl>  <dbl>  <dbl>  <dbl> <chr>  <chr>    
1 AZ-Oxford (combined)        0.694  0.558  0.806   0.95 median hdi      
2 Moderna-NIH                 0.937  0.896  0.970   0.95 median hdi      
3 Pfizer-BioNTech             0.946  0.905  0.977   0.95 median hdi      

More information

See the tidybayes documentation.