Random variables
Outline
Topics
- Random variable as mathematical objects.
- Notation convention for observation/latent
Rationale
Random variables are used as building blocks for two key uses in Bayesian stats: modelling “knowns” (observations) and “unknowns” (latent variables/parameters/prediction).
Definition
A (real) random variable is a function from a sample space \(S\) to the reals, \(X : S \to \mathbb{R}\).
Example:
- Continuing the example with \(S = \{1, 2, 3, 4\}\).
- Consider \(X(s) = 1\) if \(s\) is odd, and \(X(s) = 0\) otherwise.
Probabilist’s notation
- Let \(X\) denote a random variable.
- The notation \((X = 1)\) or \((X \in E)\) is invalid in set theory.
- Therefore, probabilists “gave it a meaning” as follows:
\[(X = 1) = \{s : X(s) = 1\}.\]
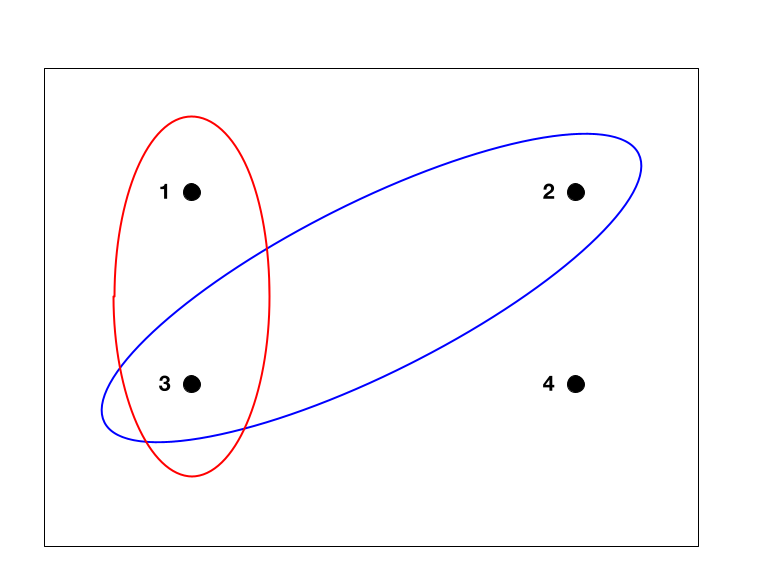
Example: Consider \(X(s) = 1\) if \(s\) is odd, and \(X(s) = 0\) otherwise. Then \((X = 1)\) corresponds to the red circle.
Conventions: probability vs Bayesian
Probability convention:
- Random variables are denoted with capitals in probability theory
- The same letter in small cap is used for a dummy variable holding the output of the random variable.
- Note: “A dummy variable holding the output of the random variable” is called a realization.
- Example: \(X\) for the random variable and \(x\) for its realization.
- We will start off using this convention in the first few weeks.
Bayesian statistics convention:
- Often the capitalization convention is not used in the Bayesian statistics literature.
- Hence we will eventually drop the probability theory capitalization convention.
More conventions
- \(X\): unobserved random variable (synonym of “unobserved”: latent)
- \(Y\): observed random variable
More precisely:
- \(Y\) is the “mechanism of observation”..
- whereas the actual observation is a realization \(y\) of \(Y\).
Extension
A random vector is a function from a sample space to \(\mathbb{R}^n\).
Example in Bayesian statistics: the vector \((X, Y)\) containing both the unobserved and observed quantities.