Axioms of probability

Partitions

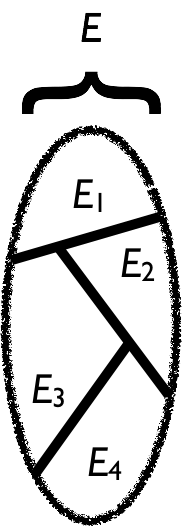
Definition: \(E_1, E_2, \dots\) is a partition of \(E\) if:

the \(E_i\)’s are disjoint, i.e., \[E_i \cap E_j = \emptyset \text{ when } i\neq j,\]
and their union is \(E\), i.e., \(\cup_i E_i = E\).

A probability is a function \(\mathbb{P}\) that satisfy the following constraints:
- \(\mathbb{P}\) should take events as input and return a number between zero and one: \[\mathbb{P}(E) \in [0, 1].\]
- Additivity axiom: if \(E_1, E_2, \dots\) is a partition of \(E\), then \[\mathbb{P}(E) = \sum_i \mathbb{P}(E_i).\]
- \(\mathbb{P}(S) = 1\)
Thanks to the constraints, even if I only specify a few known probabilities I can recover many other ones mathematically/computationally.