Decision theoretic set estimation
Outline
Topics
- Deriving a set estimate from decision theory.
Rationale
We have seen in week 2 some examples of set estimates (quantile based, highest density set).
These are actually special cases of decision theory with specific choices of loss functions.
This page provides a general framework to answer the question: “how to summarize a posterior distribution with one set?”
Context
- The weakness of point estimates is that they do not capture the uncertainty around the value.
- Idea: instead of returning a single point, return a set of points
- usually an interval,
- but this can be generalized
- Bayesian terminology: credible interval (\(\neq\) frequentist confidence intervals)
- Goals:
- We would like the credible interval to contain a fixed fraction of the posterior mass (e.g. 95%)
- At the same time, we would like this credible interval to be as short as possible given that posterior mass constraint
Bayes estimator formalization
Pick:
- \(A = \{[c, d] : c < d\}\),
- consider the loss function given by \[ L([c, d], x) = \mathbb{1}\{x \notin [c, d]\} + k (d - c) \] for some tuning parameter \(k\) to be determined later.
We get:
\[ \begin{aligned} \delta_{\text{B}}(Y) &= \operatorname{arg\,min}\{ \mathbb{E}[L(a, X) | Y] : a \in A \} \\ &= \operatorname{arg\,min}\{ \Pr[X \notin [c, d] | Y] + k(d - c) : [c,d] \in A \} \\ &= \operatorname{arg\,min}\{ \Pr[X < c|Y] + \Pr[X > d |Y] + k(d - c) : [c,d] \in A \} \\ &= \operatorname{arg\,min}\{ \Pr[X \le c|Y] - \Pr[X \le d |Y] + k(d - c) : [c,d] \in A \} \end{aligned} \]
Here we assume the posterior has a continuous density \(f\) to change \(<\) into \(\le\).
As we did with point estimation, we take the derivative with respect to \(c\) and set to zero (then will do the same thing for \(d\)).
Notice that \(\Pr[X \le c|Y]\) is the posterior cumulative distribution function (CDF)1, so taking the derivative with respect to \(c\) yields a density:2
\[ f_{X|Y}(c) - k = 0, \]
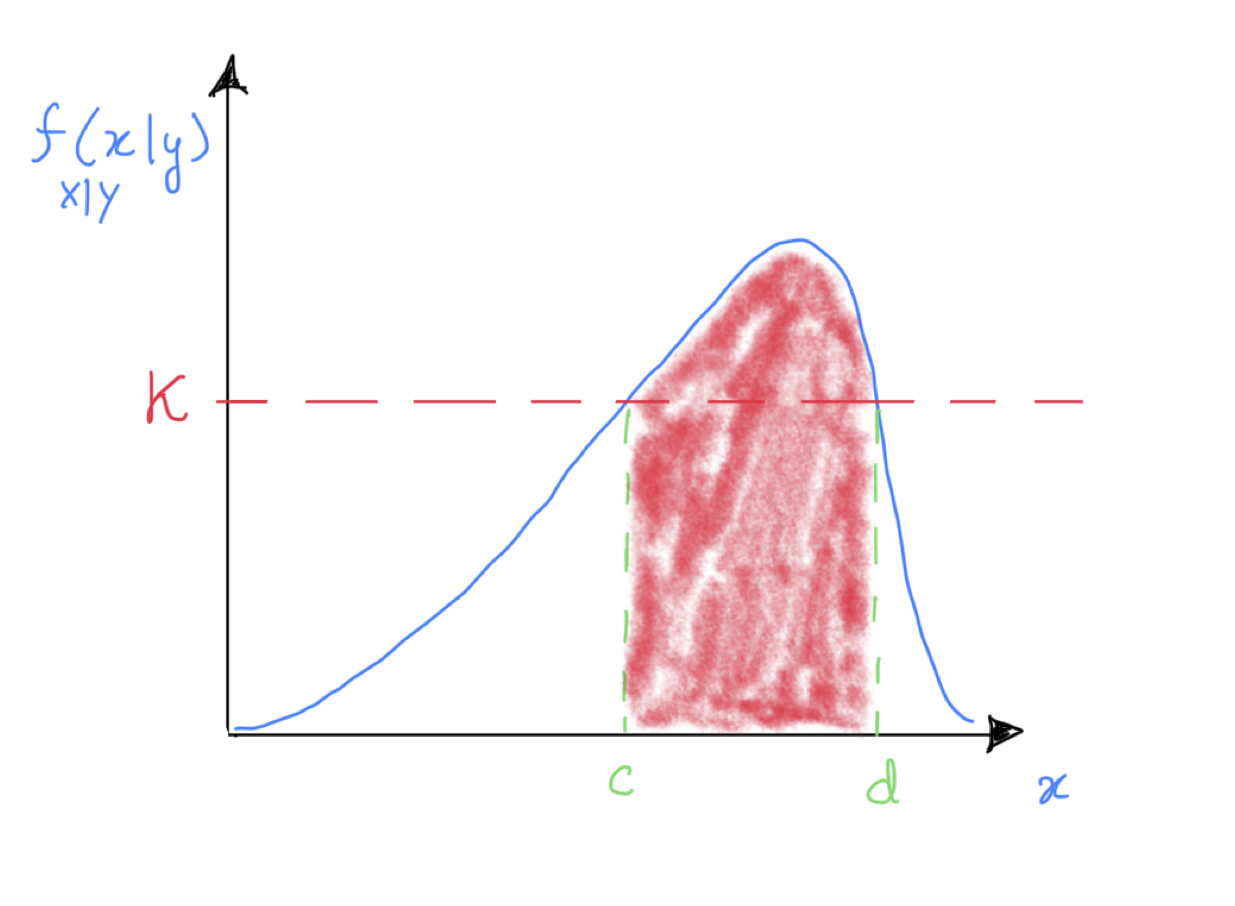
so we see the optimum will be the smallest interval \([c, d]\) such that \(f(c) = f(d) = k\).
Finally, set \(k\) to capture say 95% of the mass (area in red in the figure shows a 50% example, we would lower \(k\) to get to 95%).
Footnotes
Recall that a CDF is defined as \(F(x) = \mathbb{P}(X \le x)\). So a posterior CDF is just \(\mathbb{P}(X \le x | Y)\).↩︎
Let us review the argument why “taking the derivative … yields a density”. Let \(f\) denote a density and \(F\), the CDF of the same random variable. From the definition of a density, \(F(x) = \int_{-\infty}^x f(x') \mathrm{d}x'\) (i.e., take \(A = [-\infty, x]\) in the definition of a density). Hence by the Fundamental theorem of calculus (i.e. the fact that an integral is an “anti-derivative”), we have that \[f(x) = \frac{\mathrm{d}F(x)}{\mathrm{d}x},\] when the derivative exists.↩︎