Bernoulli regression

Outline

Topics

  • A first example of a Bayesian model based on a linear model and a Bernoulli likelihood.
  • Prior construction via prior predictive distribution.
  • Approximation of the posterior using a PPL.
  • Visualizing a posterior distribution over functions.

Rationale

  • This is our first example of a Bayesian General Linear Model (GLM).
  • GLMs are the probably the most common models.

Example

source("../../solutions/simple.R")
source("../blocks/simple_utils.R")
suppressPackageStartupMessages(require("dplyr"))
set.seed(1)

df = read.csv("../data/launches.csv") %>% filter(LV.Type == "Ariane 1")
success_indicators = df$Suc_bin
rmarkdown::paged_table(df)
plot(success_indicators, xlab = "Launch index i")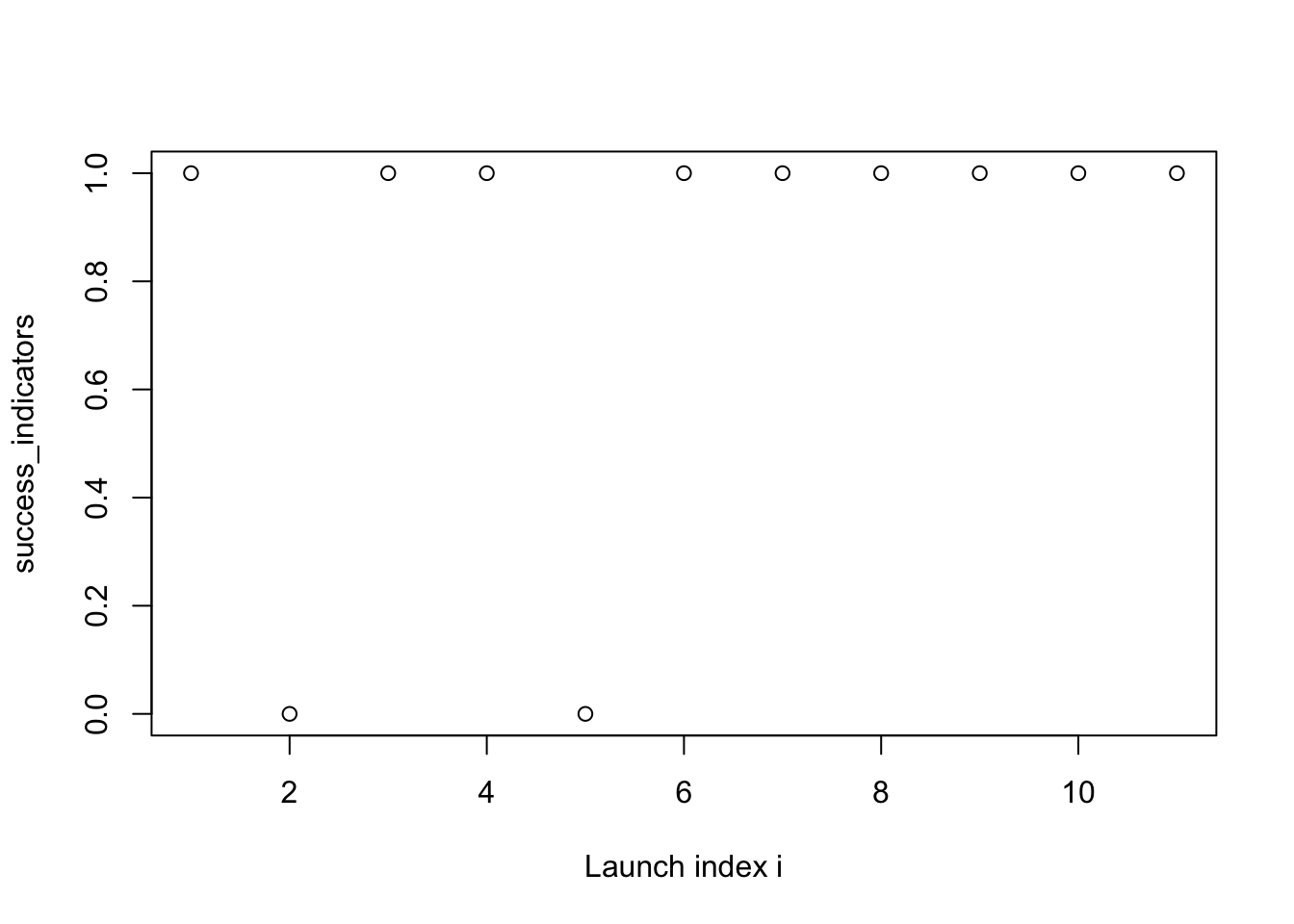

  • From this “Exploratory Data Analysis” (EDA), it seems plausible that the success probability is increasing with time.
  • Matches with intuition: after a failure, some corrections are made.

Building a better model

  • Each observation is binary, so the likelihood still has to be Bernoulli.
    • We will denote its parameter by \(\theta \in [0, 1]\).
  • What we will change is the prior.
  • Old model: \(\theta\) is shared by all launches (“constant over the launch index” \(i \in \{1, 2, \dots, 11\}\))
  • New model: \(\theta\) changes from one launch to the next.
    • i.e., \(\theta\) is a function of the index \(i \in \{1, 2, \dots, 11\}\), denoted \(\theta(i)\).
    • Question: what kind of function should we start with?

General modelling principle: start with something simple!

In our context: start with a linear function.

Structure of the model

  • We need to build a prior over linear functions.
  • Recall: enough to describe how to forward simulate a dataset.
  • Forward simulation process:
    1. simulate an intercept,
    2. simulate a slope,
    3. this determines \(\theta(i)\) for each \(i \in \{1, 2, \dots, 11\}\).
    4. Simulate \(y_i \sim {\mathrm{Bern}}(\theta(i))\) independently but not identically.
  • I.e. we have reduce the problem to that of sampling two real numbers.

Prior (first attempt)

Let us draw one random linear function:

  • Math: (not yet final) \[\begin{align*} \text{slope} &\sim \mathcal{N}(0, 1) \\ \text{intercept} &\sim \mathcal{N}(0, 1) \\ \theta(i) &= \text{slope} \cdot i + \text{intercept} \end{align*}\]
  • Forward simulation code: (not yet final)
set.seed(1)
plot(success_indicators, ylab = "success probability", xlab = "Launch index i")
xs = 1:length(success_indicators)
intercept = simulate(Norm(0, 1))
slope     = simulate(Norm(0, 1))

lines(intercept + slope * xs)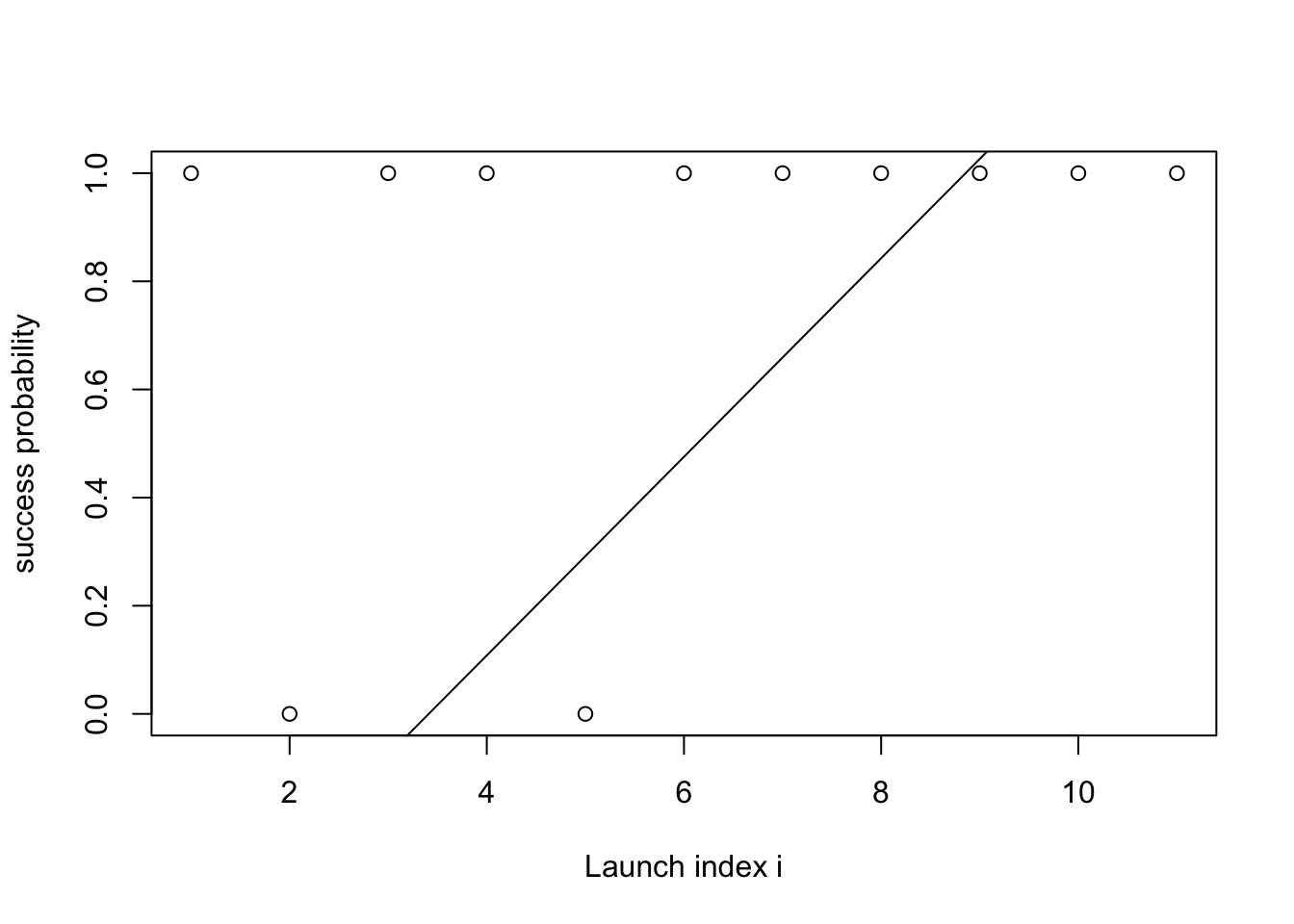

What is the problem in the above?

  • The function \(\theta(i)\) can take values smaller than zero or greater than one.
  • This creates problem when we feed the parameter to the Bernoulli, which expects a number between 0 and 1.

Fix:

  • we cannot use just a linear function…
  • … instead we can compose a linear function with the logistic or sigmoid function.
    • Logistic function: maps real numbers \(r \in (-\infty, \infty)\) into \((0, 1)\).
    • Math: \[\text{logistic}(r) = \frac{1}{1 + e^{-r}}.\]
    • In R: plogis(r).
rs = seq(-5, 5, 0.01)
plot(rs, plogis(rs), type = 'l', xlab = "r", ylab = "logistic(r)")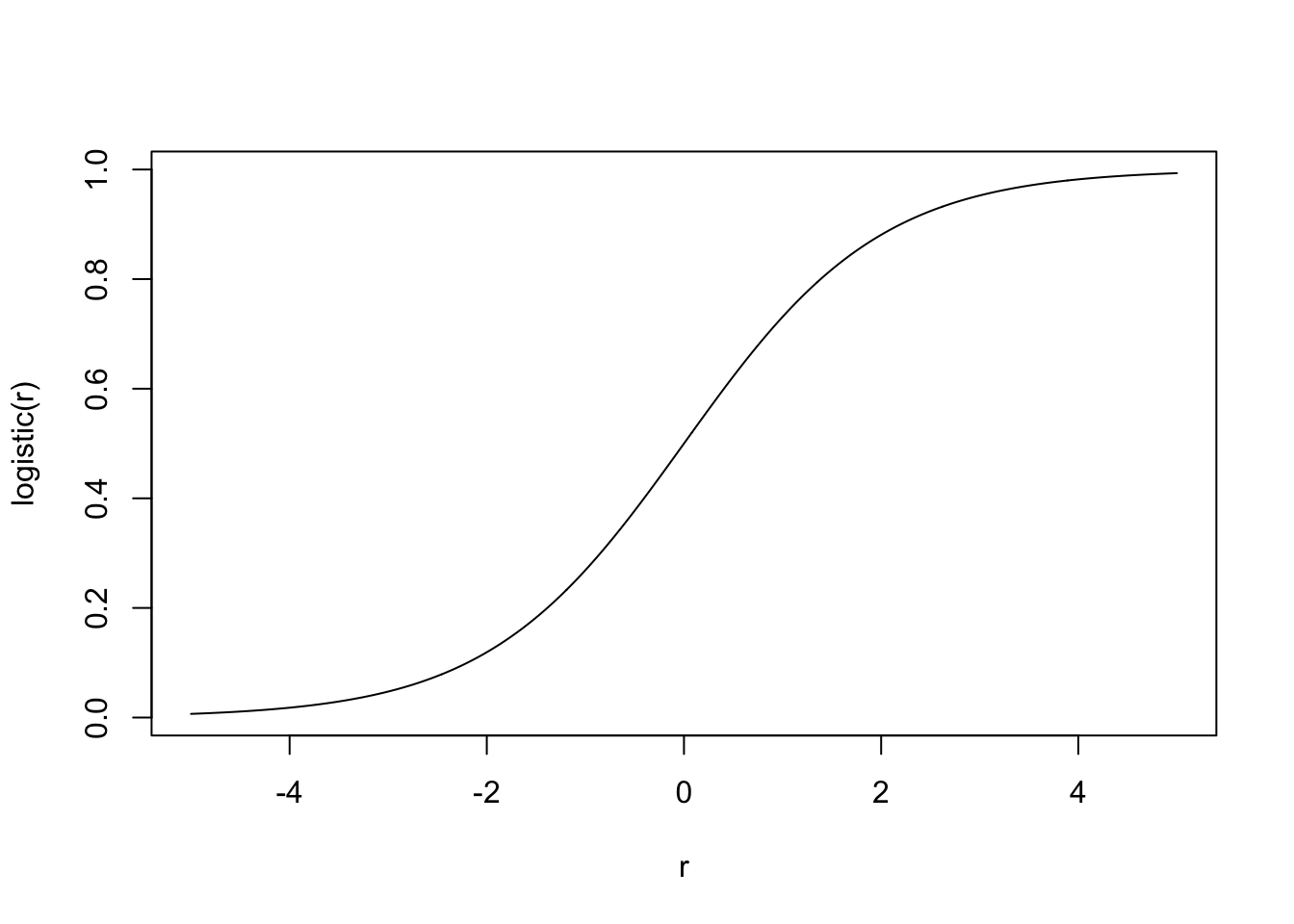

Prior (second, final attempt)

  • Math: \[\begin{align*} \text{slope} &\sim \mathcal{N}(0, 1) \\ \text{intercept} &\sim \mathcal{N}(0, 1) \\ \theta(i) &= \text{logistic}(\text{slope} \cdot i + \text{intercept}) \end{align*}\]
  • Forward simulation code:
set.seed(1)
plot(success_indicators, ylab = "success probability", xlab = "Launch index i")
xs = 1:length(success_indicators)
intercept = simulate(Norm(0, 1))
slope     = simulate(Norm(0, 1))

lines(plogis(intercept + slope * xs))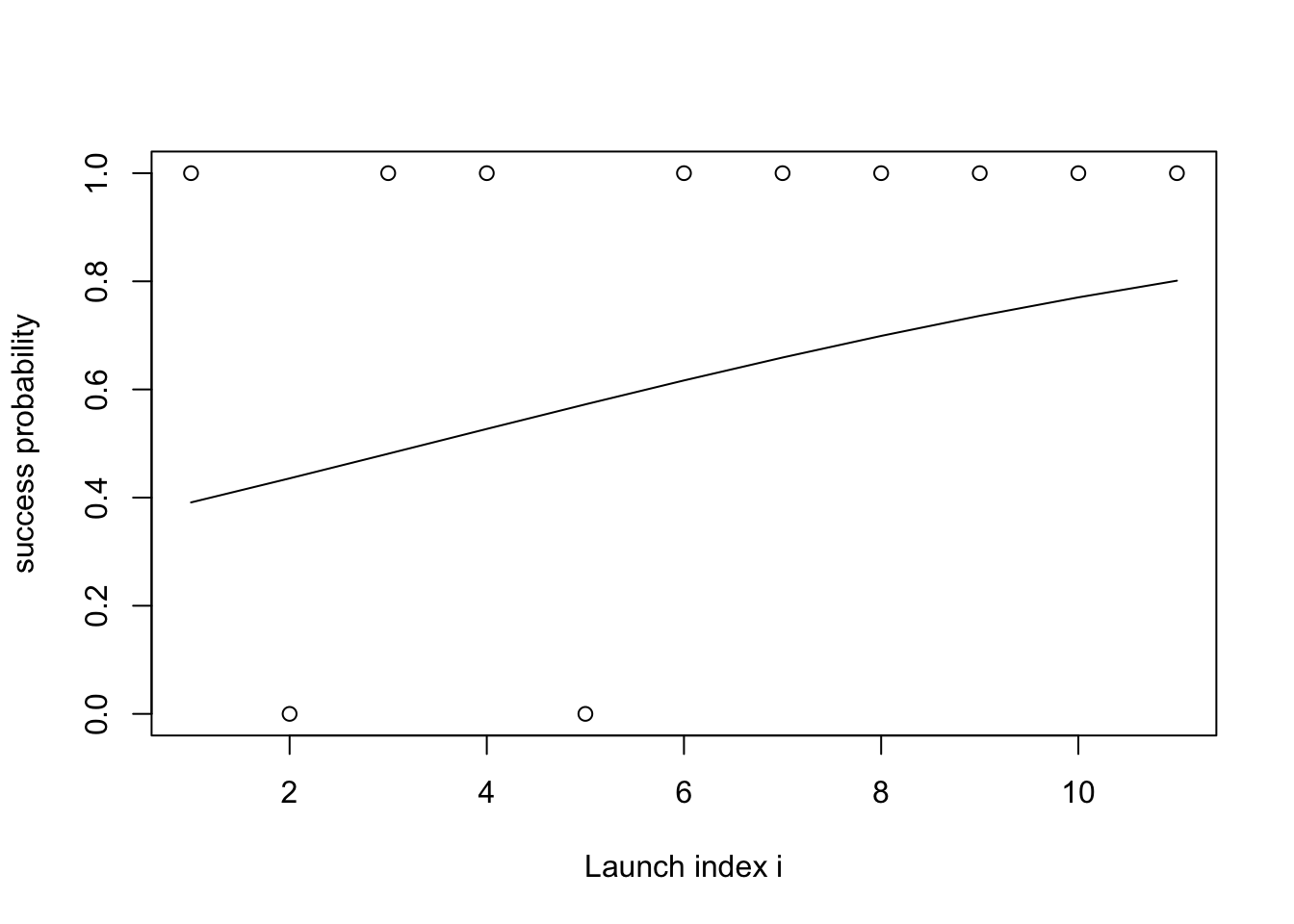

Prior predictive

Let us repeat what we did in the last section 50 times to see several draws from the prior at once (using alpha to make the lines translucent):

set.seed(1)
plot(success_indicators, ylab = "success probability", xlab = "Launch index i")
xs = 1:length(success_indicators)

for (i in 1:50) {
  intercept = simulate(Norm(0, 1))
  slope     = simulate(Norm(0, 1))
  lines(plogis(intercept + slope * xs), col = rgb(red = 0, green = 0, blue = 0, alpha = 0.5))
}

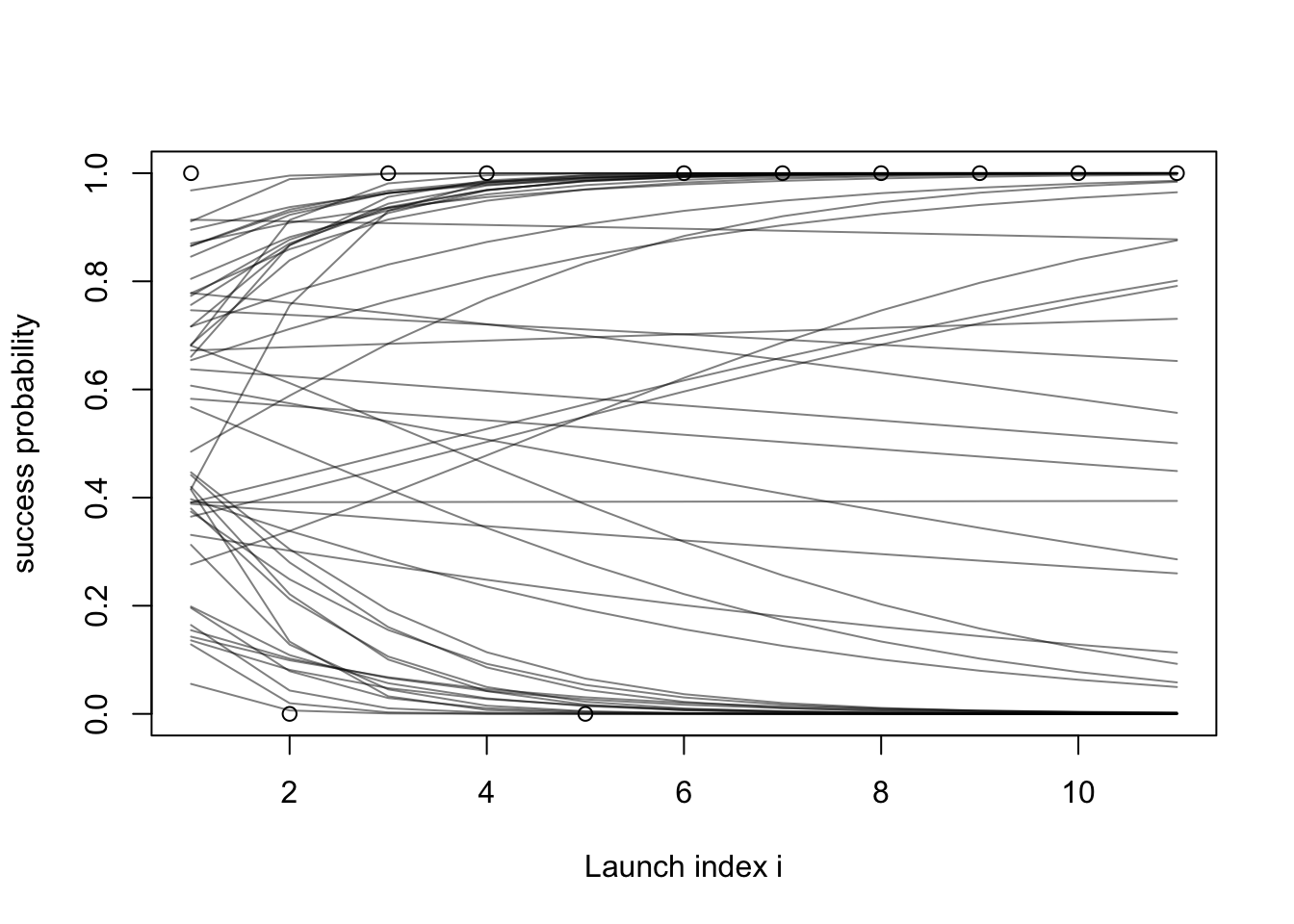
  • Hard to get intuition about a prior by just staring at the mathematical formulas.
  • Simulating from the prior can help figuring out if the prior is reasonable or not.
    • This is known as the prior predictive.
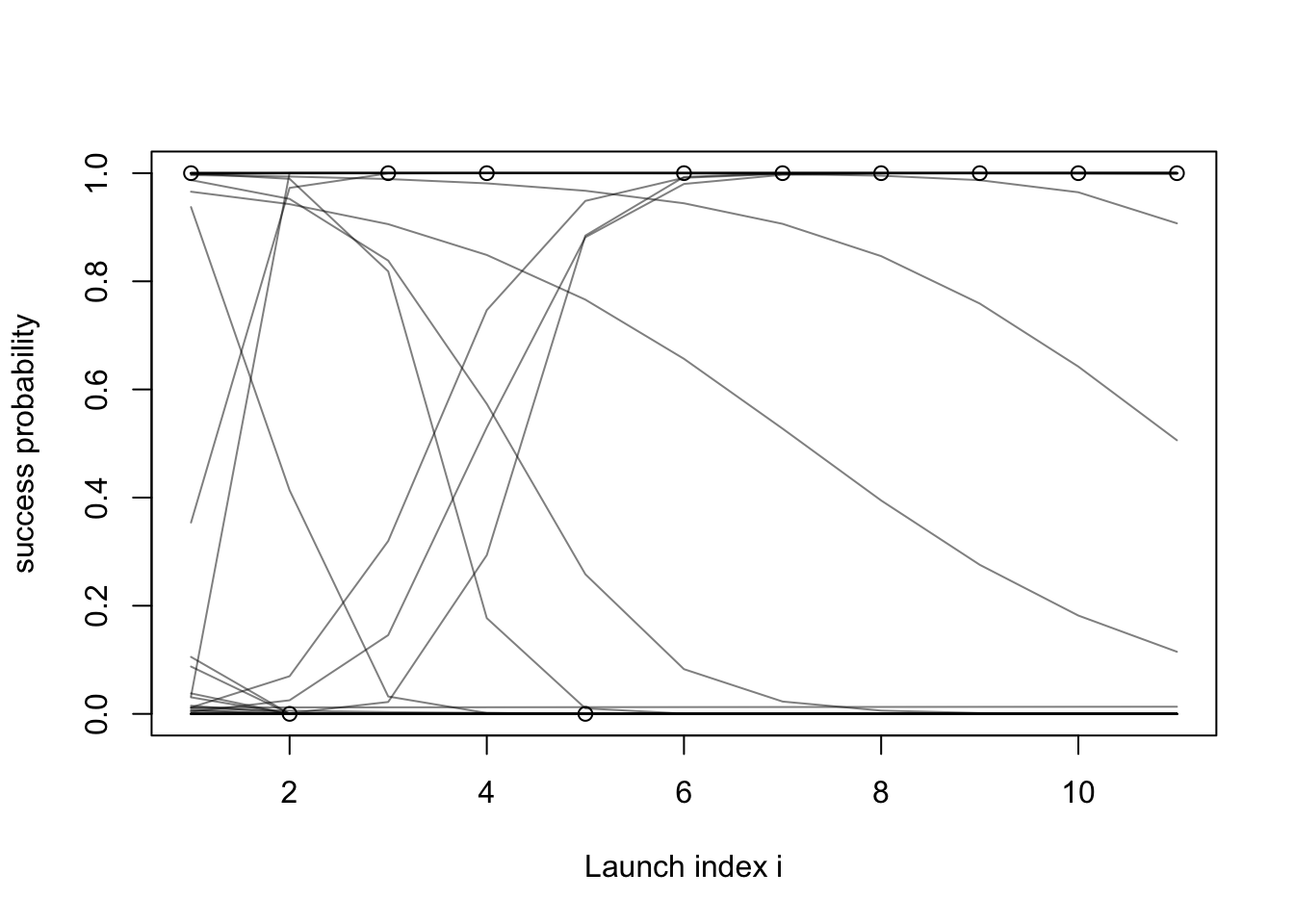
  • Exploration:
    • so far I used a mean of zero and standard deviation of 1 for the slope and intercept priors.
    • Let us try a prior that is more “vague”, with standard deviation of 10 for both the slope and intercept priors:
set.seed(1)
plot(success_indicators, ylab = "success probability", xlab = "Launch index i")
xs = 1:length(success_indicators)

for (i in 1:50) {
  intercept = simulate(Norm(0, 10))
  slope     = simulate(Norm(0, 10))
  lines(plogis(intercept + slope * xs), col = rgb(red = 0, green = 0, blue = 0, alpha = 0.5))
}

Posterior distribution

  • In this week’s exercise, you will implement the model described above in simPPLe.
  • Here is a peak of the posterior distribution you should obtain:
source("../../solutions/sol04_logistic_regression.R")

posterior = posterior_particles(logistic_regression, 1000)
weighted_scatter_plot(posterior, plot_options = list(xlab="intercept parameter", ylab="slope parameter"))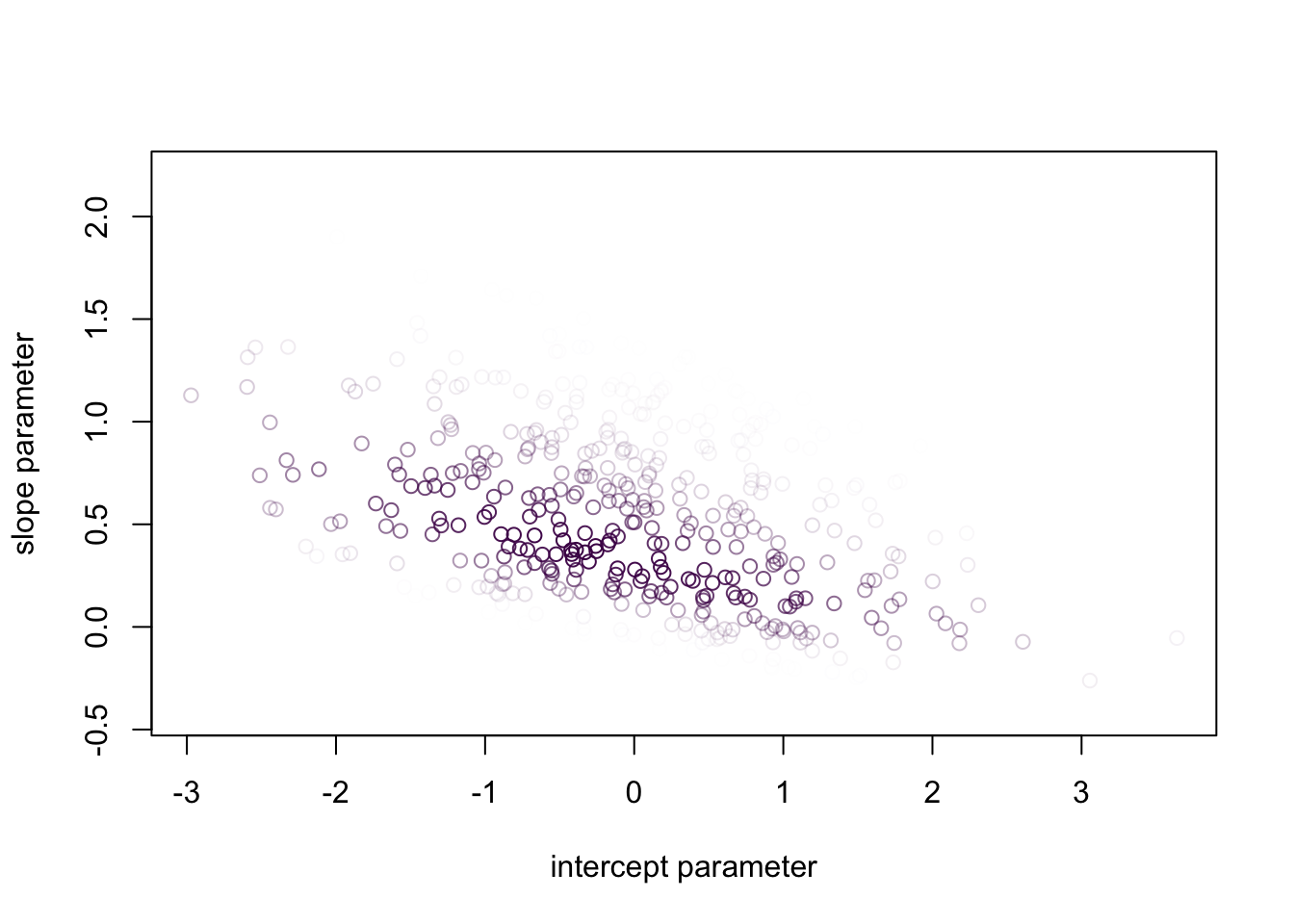

  • Again, this is a bit hard to interpret.
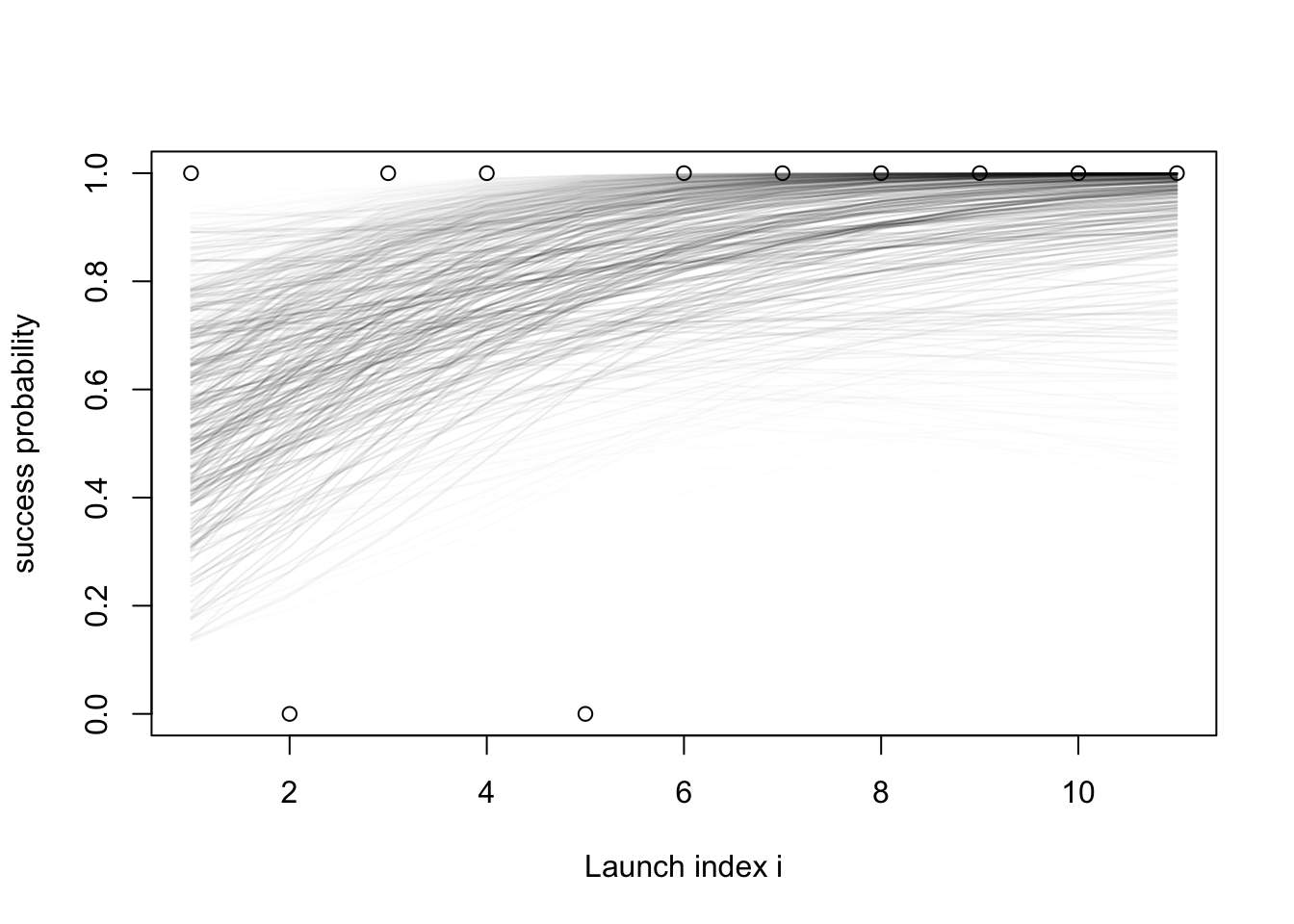
  • Let us plot similarly to what we did with the prior predictive:
    • For each sample \(x^{(m)}= (\text{intercept}^{(m)}, \text{slope}^{(m)})\) with weight \(w^{(m)}\),
    • Draw the curve \(\text{logistic}(\text{slope}^{(m)}\cdot i + \text{intercept}^{(m)})\)…
    • with alpha value (transparency) proportional to the corresponding weight \(w^{(m)}\).
set.seed(1)
plot(success_indicators, ylab = "success probability", xlab = "Launch index i")
xs = 1:length(success_indicators)

samples = posterior$samples 
norm_weights = posterior$weights / sum(posterior$weights)

for (i in 1:nrow(samples)) {
  intercept = samples[i, 1]
  slope     = samples[i, 2]
  pr = norm_weights[i]
  lines(plogis(intercept + slope * xs), col = rgb(red = 0, green = 0, blue = 0, alpha = pr*20))
}

Terminology

The model we just reviewed is an instance of Bayesian logistic regression, a method for classification.

Some terminology from classification:

  • output variables: instances of which we try to “predict”
    • also known as “target”, “label”, “predicted variable”, “regressand”, …
    • sometimes observed (“training instances”), sometimes unobserved (“test instances”)
    • in our example?
  • input variables: what we use as the basis of each prediction
    • also known as “independent variables”, “covariates”, “predictor”, “regressors”, “feature”,..
    • typically always observed (both at training and test time)
  • parameters: auxiliary quantities that encode a function mapping inputs to (information on) output.

References