suppressPackageStartupMessages(require(rstan))More Bayesian bricks
Outline
Topics
- More distributions to complement those tested in quiz 1.
- Motivation, realization and parameterization(s) for each.
- Reparameterization.
Rationale
Recall our model building strategy:
- start with observation, and find a distribution that “match its data type” (this creates the likelihood),
- i.e. such that support of the distribution \(=\) observation data type
- then look at the data types of each of the parameters of the distribution you just picked…
- …and search for a distributions that match each the parameters’ data type (this creates the prior),
- in the case of hierarchical models, recurse this process.
There are a few common data types for which we do not have talked much about distributions having realizations of that datatype. We now fill this gap.
Counts
- Support: \(\{0, 1, 2, 3, \dots\}\).

- Simple common choice is the Poisson distribution:
- \({\mathrm{Poisson}}(\lambda)\)
- Parameter: Mean \(\lambda > 0\).
- Motivation: law of rare events.
- Stan doc.
- \({\mathrm{Poisson}}(\lambda)\)
- Popular alternative, e.g., in bio-informatics: the negative binomial distribution:
- \({\mathrm{NegBinom}}(\mu, \phi)\)
- Mean parameter \(\mu > 0\) and concentration \(\phi > 0\).
- Motivation:
- Poisson’s variance is always the same as its mean.
- Consider \({\mathrm{NegBinom}}\) when empirically the variance is greater than the mean (“over-dispersion”).
- Stan doc.
Positive real numbers
- Support: \(\{x \in \mathbb{R}: x > 0\} = \mathbb{R}^+\)
- More common choice is the gamma distribution:
- \({\mathrm{Gam}}(\alpha, \beta)\)
- Parameters: Shape parameters \(\alpha > 0\) and rate \(\beta > 0\).
- Stan doc.
Question: consider the following Stan model:
data {
int<lower=0> n_obs;
vector<lower=0>[n_obs] observations;
}
parameters {
real<lower=0> shape;
real<lower=0> rate;
}
model {
// priors
shape ~ exponential(1.0/100);
rate ~ exponential(1.0/100);
// likelihood
observations ~ gamma(shape, rate);
}Notice that neither of the parameters passed in the likelihood can be interpreted as a mean. However, you are asked to report a mean parameter for the population from which the observations come from. How would you proceed?
Categories
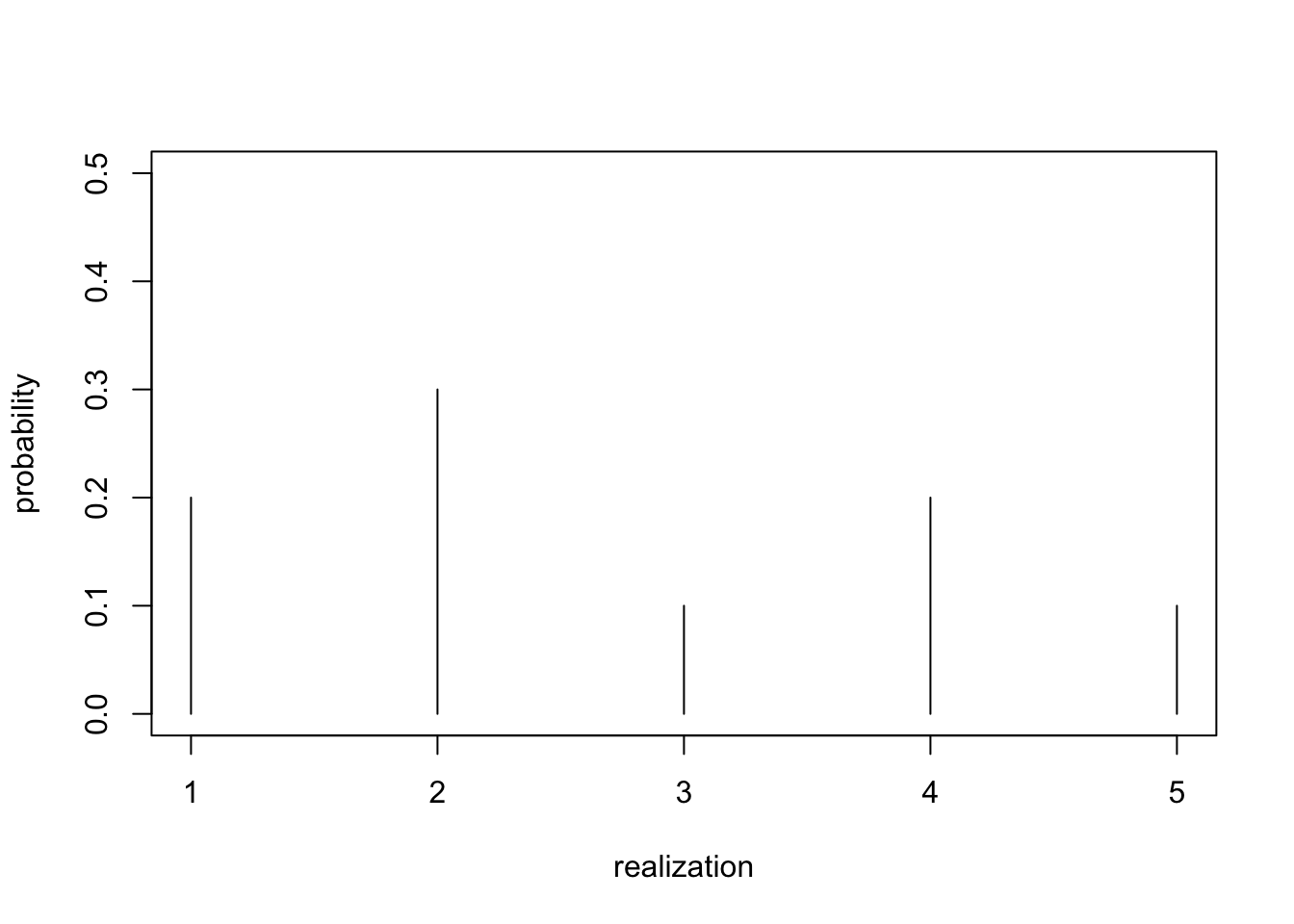
- Support: \(\{0, 1, 2, 3, \dots, K\}\), for some number of categories \(K\).
- All such distributions captured by the categorical distribution
- We first discussed it in Exercise 3.
- \({\mathrm{Categorical}}(p_1, \dots, p_K)\)
- Probabilities \(p_k > 0\), \(\sum_k p_k = 1\).
- Stan doc.
Simplex
Terminology for the set of valid parameters for the categorical, \(\{(p_1, p_2, \dots, p_K) : p_k > 0, \sum_k p_k = 1\}\): the \(K\)-simplex.
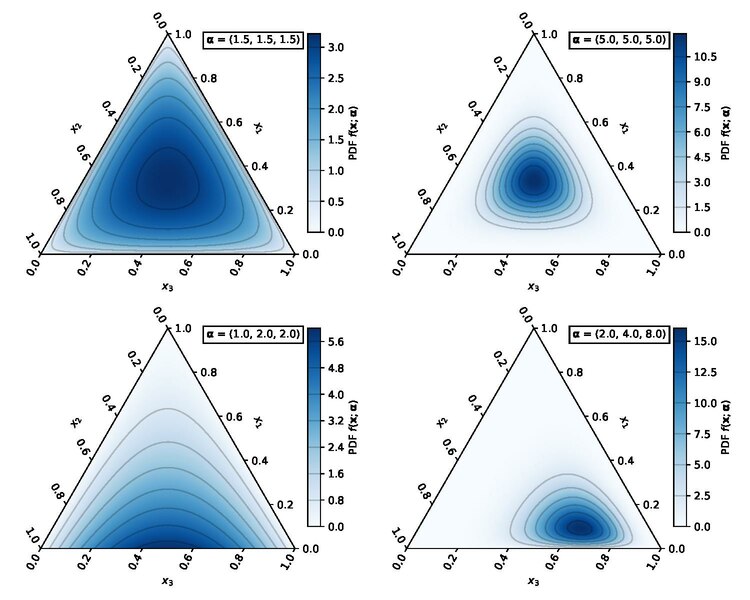
- Hence, if you need a prior over the parameters of a categorical, you need a distribution over the simplex!
- Common choice: the Dirichlet distribution:
- \({\mathrm{Dir}}(\alpha_1, \dots, \alpha_K)\)
- Concentrations \(\alpha_i > 0\).
- Stan doc.
Vectors
- Support: \(\mathbb{R}^K\)
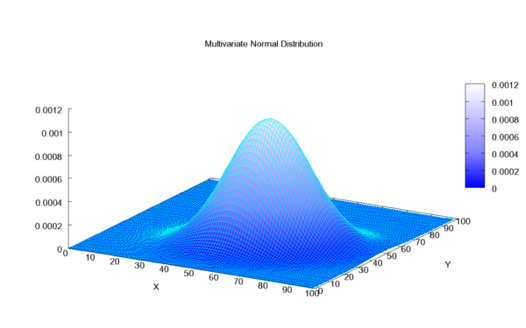
- Common choice: the multivariate normal.
- \(\mathcal{N}(\mu, \Sigma)\)
- Mean vector \(\mu \in \mathbb{R}^K\), covariance matrix \(\Sigma \succ 0\), \(\Sigma\) symmetric.
- Stan doc.
Many others!
References
- Use wikipedia’s massive distribution list,
- and Stan’s documentation.
Alternative approach: reparameterization
- Suppose you need a distribution with support \([0, 1]\).
- We have seen above that one option is to use a beta prior.
- An alternative:
- define \(X \sim \mathcal{N}(0, 1)\),
- use a transformation to map it to \([0, 1]\), e.g. \(Y = \text{logistic}(X)\).
- This approach is known as “re-parametrization”
- For certain variational approaches, this helps inference.
- More on that in the last week.