Balance equations

Outline

Topics

• Global balance (synonym: invariance)
• Detailed balance (synonym: time-reversibility)

Rationale

We need formulas to help us prove that MH is \(\pi\)-invariant (and hence combined with irreducibility, admits a LLN).

Example

We continue our eccentric tourists example…

Question: which travelling scheme(s) are \(\pi\)-invariant?

Intuition: \(\pi\)-invariance in this context just means the fraction of tourists in each city will stay constant over time.

1. Pairs of cities, where each pair of cities is assigned a fixed number of planes going back and forth between the two cities (see figure, planes always full).
2. A tour where a fixed number of planes, equal to the number of cities, go around the world on a common route (see figure, again, planes always full).
3. A central “hub”, where all flights land at the hub (see figure, again, planes always full).

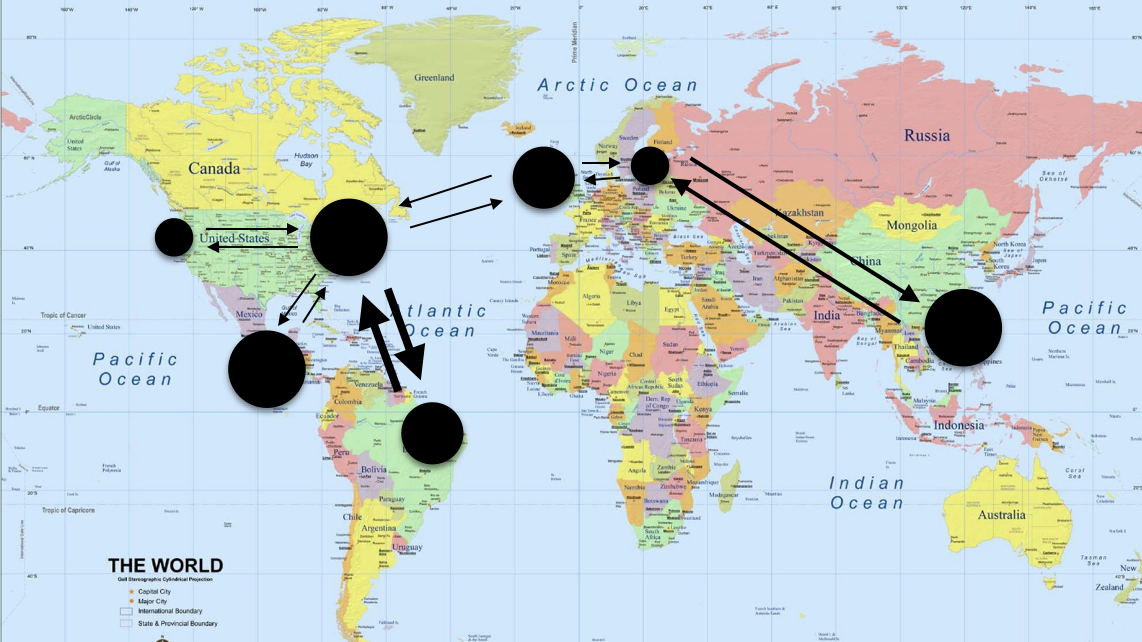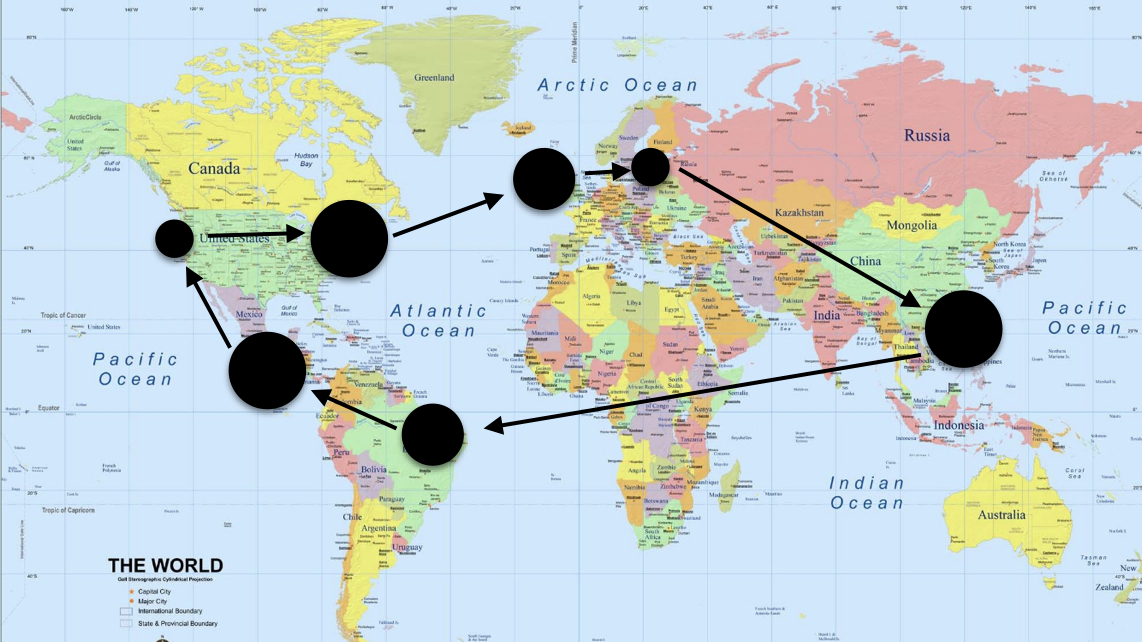a: b: c: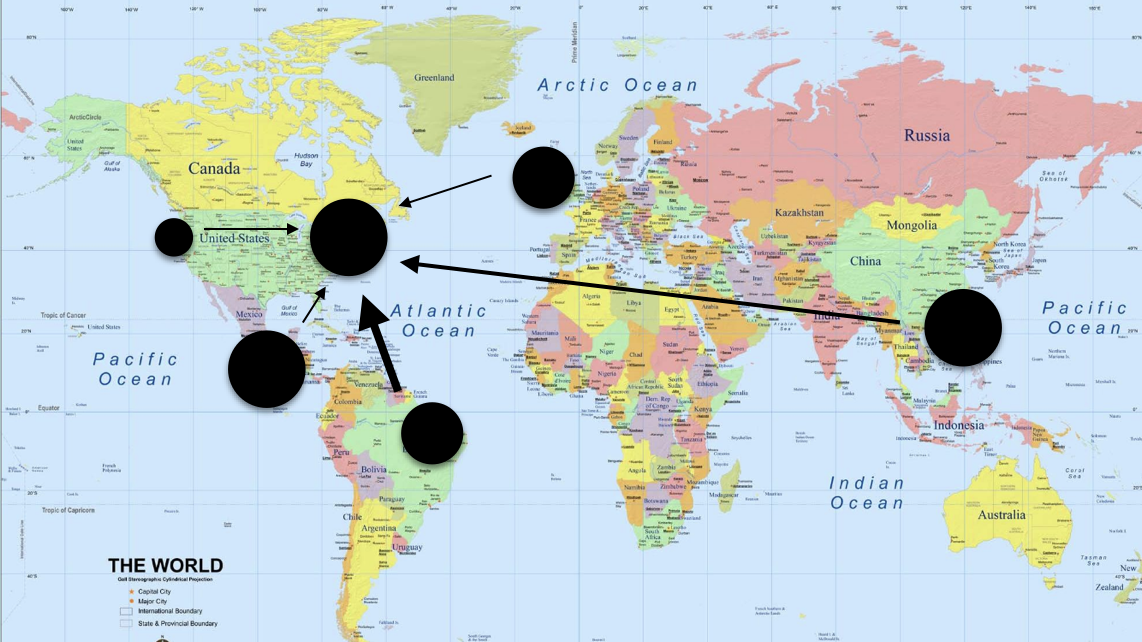

Global balance

Question: combine

• the definition of \(\pi\)-invariance, with
  
• the formula we derived for the marginals of a Markov chain, i.e., \[\mu_2(x') = \sum_x \mu_1(x) K(x' | x),\]

to get an equation characterizing \(\pi\)-invariance in terms of \(K\).

Detailed balance

Question: write mathematically “pairs of cities, where each pair of cities is assigned a fixed number of planes going back and forth between the two cities (planes always full).”

Relationship between detailed and global balance

Question: what is the relationship between local and global balance? Does one imply the other?