Marginals of a Markov chain
Outline
Topics
- Computing a marginal of a Markov chain.
Rationale
The notion of invariance is formally expressed using marginals of a Markov chain. To check invariance we need formulas to write marginals of Markov chains.
Example
- Consider a large group of identical tourists.
- They travel the world in a finite set of cities (dots).
- Every weekend they can board a plane and go somewhere else.
- They base their choice of destination only on the current city.
- They use randomness (e.g., if a tourist is in London, flip a coin to decide to go to Montreal or Stockholm).
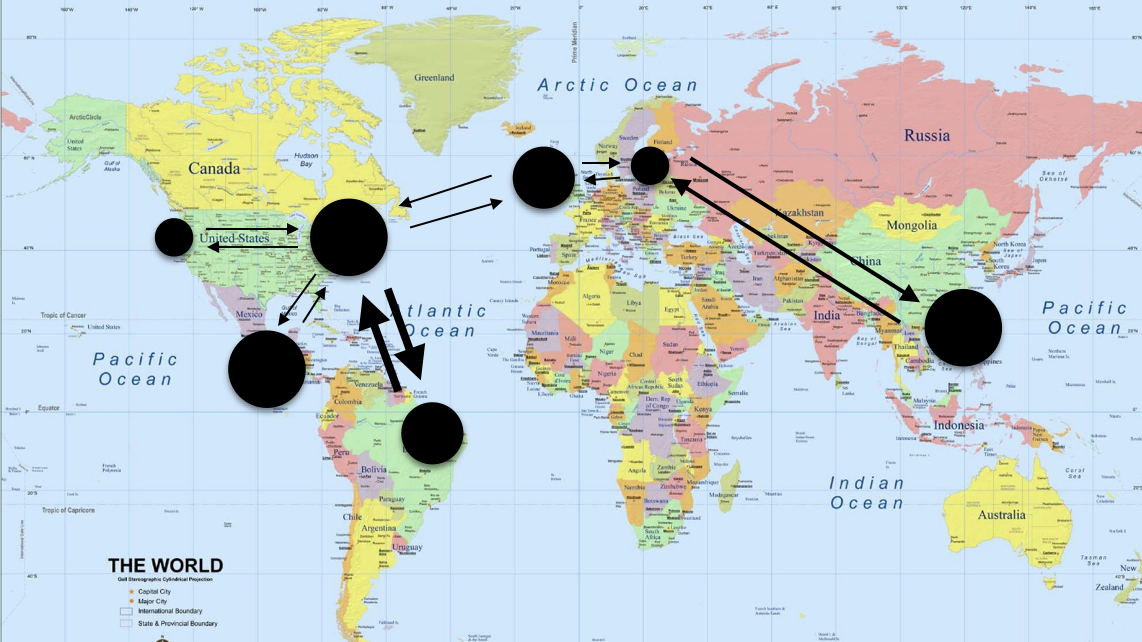
Markov model for random tourists
- \(X^{(1)}\): pick one of the tourists at random, \(X^{(1)}\) encodes the city this tourist is in at week 1 (before taking a first flight).
- Distribution of \(X^{(1)}\): \(\mu_1(x)\).
- Interpretation: for city \(x\), \(\mu_1(x)\) tells you the fraction of tourists in city \(x\) on the first week.
- Size of the dots in the figure is the fraction of tourists in the city.
Review: what is the name of the distribution of \(X^{(1)}\)?
Click for answer
The initial distribution.
- \(K(x'|x)\) encodes the probability that a tourist move to city \(x'\) next week given they are at \(x\) this week.
- \(X^{(2)} \sim K(\cdot|X^{(1)})\).
- On the second week, some cities may now have more or less tourists.
- Distribution of \(X^{(2)}\): \(\mu_2(x)\).
- Interpretation: for city \(x\), \(\mu_2(x)\) tells you the fraction of tourists in city \(x\) on the second week.
Marginal of a Markov chain
Definition
Definition: the distribution on \(X^{(m)}\) is called the marginal, denoted \(\mu_m(x)\).
Computing a marginal
Question: write the marginal distribution at step 2, \(\mu_2\) using \(\mu_1\) and \(K\).