Stan: hands on

Outline

We revisit the time-varying Ariane 1 rocket failure probability model to practice the Stan syntax introduced this week.

suppressPackageStartupMessages(require(rstan))
suppressPackageStartupMessages(require(ggplot2))
suppressPackageStartupMessages(require(dplyr))

set.seed(1)

df = read.csv(url("https://raw.githubusercontent.com/UBC-Stat-ML/web447/main/data/launches.csv")) %>% filter(LV.Type == "Ariane 1")
success_indicators = df$Suc_bin
rmarkdown::paged_table(df)

plot(success_indicators, xlab = "Launch index i")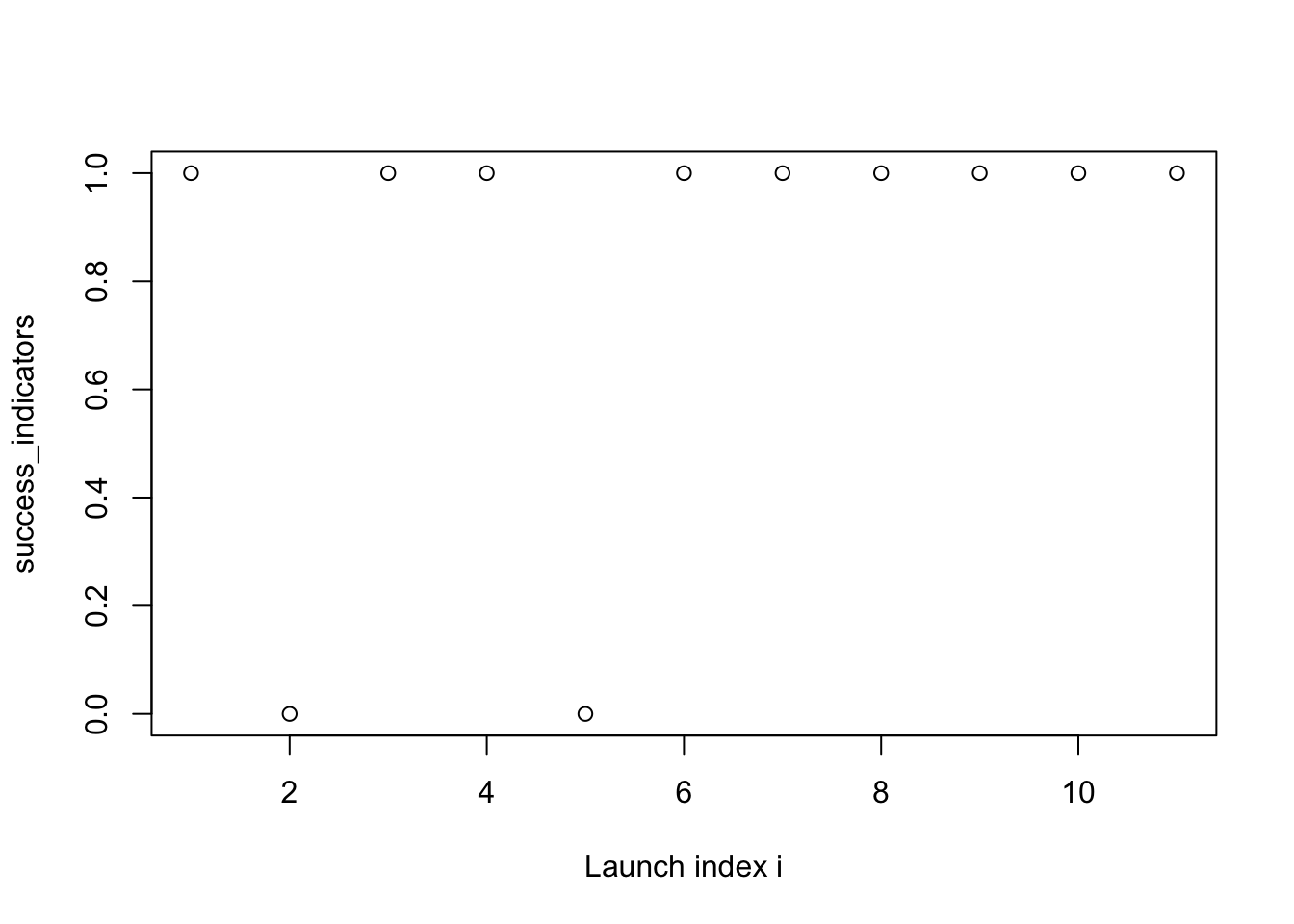

Model

Recall the model we discussed previously (with the difference that we use a SD of 10 now)

\[\begin{align*} \text{slope} &\sim \mathcal{N}(0, 10) \\ \text{intercept} &\sim \mathcal{N}(0, 10) \\ \theta(i) &= \text{logistic}(\text{slope} \cdot i + \text{intercept}) \\ y_i &\sim {\mathrm{Bern}}(\theta(i)) \end{align*}\]

…which you also implemented in simPPLe as part of exercise 4:

logistic_regression = function() {
  intercept = simulate(Norm(0, 10))
  slope     = simulate(Norm(0, 10))
  for (i in seq_along(success_indicators)){
    success_probability = plogis(intercept + i*slope)
    observe(success_indicators[i], Bern(success_probability))
  }
  return(c(intercept, slope))
}

Translation into Stan

Question 1: use the template below to translate the above model into Stan. Set the seed to 1, run 10000 MCMC iterations, and report the posterior mean of the slope parameter.

data { 
  int N; 
  array[N] int y; 
}

parameters { 
  real slope;
  real intercept;
}

model {
  // complete this
}

Using the posterior

Question 2: compute a 95% credible interval on the slope parameter.

Hint

Use the output of println on the fit object.

Question 3: translate “your updated belief that the Ariane 1 rockets were improving” into a mathematical expression.

Question 4: estimate the numerical value of the expression in the last question.