Conditioning

Outline

Topics

• Intuition on conditioning
• A conditional probability is a probability.

Rationale

• Conditioning is the workhorse of Bayesian inference!
  • Used to define models (as when we assigned probabilities to edges of a decision tree)
  • And soon, to gain information on latent variables given observations.

Conditioning as belief update

Key concept: Bayesian methods use probabilities to encode beliefs.

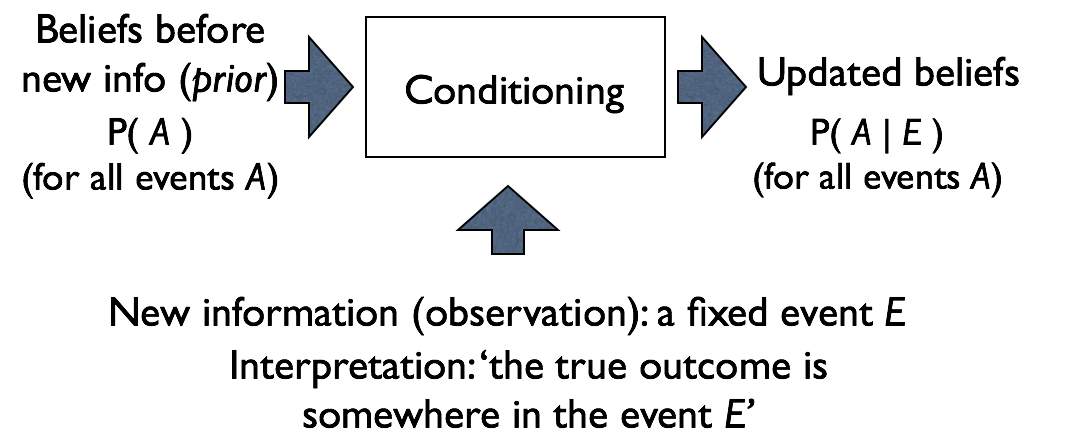
We will explore this perspective in much more details next week.

A conditional probability is a probability

The “updated belief” interpretation highlights the fact that we want the result of the conditioning procedure, \(\mathbb{P}(\cdot | E)\) to be a probability when viewed as a function of the first argument for any fixed \(E\).

Intuition behind conditioning

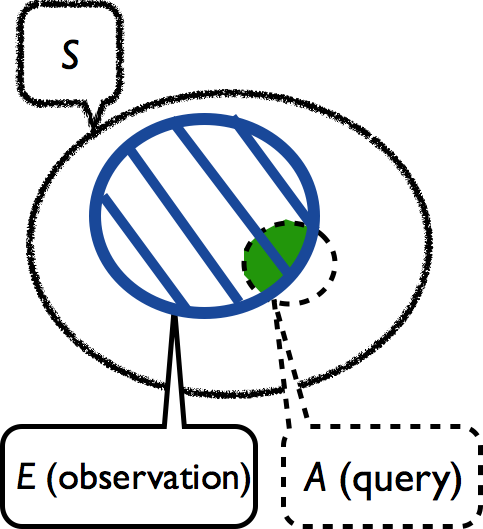
• For a query even \(A\), what should be the updated probability?
• We want to remove from \(A\) all the outcomes that are not compatible with the new information \(E\). How?
  • Take the intersection: \(A \cap E\)
  • We also want: \(\mathbb{P}(S | E) = 1\) (last section)
  • How? Renormalize: \[\mathbb{P}(A | E) = \frac{\mathbb{P}(A \cap E)}{\mathbb{P}(E)}\]
  • Intersection can also be denoted using a comma, for example \(\mathbb{P}(A \cap E) = \mathbb{P}(A, E)\)