Intro to hierarchical models

Outline

Topics

  • Hierarchical models.
  • Intuition why they decrease prior sensitivity.

Rationale

Hierarchical models, a crowning achievement of Bayesian inference, can be used to decrease prior sensitivity even when the dataset of interest is of limited size.

Example

Example: predicting the probability of failure of the next Delta 7925H launch (so far, we observed this type of rocket has been launched 3 times, with 0 failed launches).

Key idea: use “side data” to inform the prior…

  • For example: success/failure launch data from other other types of rockets.
  • Can we use the following rocket launch dataset to inform prediction for a single rocket type of interest?
suppressPackageStartupMessages(require("dplyr"))
df = read.csv("../data/failure_counts.csv") 
rmarkdown::paged_table(df)

How to use “side data”? Two suboptimal approaches

For pedagogy, we will first cover two simple heuristics to incorporate “side data” and describe their limitations.

Then we will cover hierarchical models in the next section, showing how they address the limitations of simpler methods.

First try (do not use this one!)

  • Merge all the data into one type?
  • I.e. just sum the columns in the data:
sum(df$numberOfLaunches)
[1] 5667
sum(df$numberOfFailures)
[1] 431

Why merging everything is a bad idea?

Some of these types of rockets are very different than the one under study (Delta 7925H). For example some of them are very old, made by different space agencies, etc.

An indeed, the aggregated failure rate is high compared to what you would expect from modern “workhorse” rockets (<1%):

sum(df$numberOfFailures) / sum(df$numberOfLaunches)
[1] 0.07605435

We want to consider the different types of rockets as a population and model the variability within that population.

Towards an improved way to use side data

  • Background: “mean–pseudo-sample-size” reparameterization of the Beta distribution.
    • A reparametrization is a different labelling of a family such that you can go back and forth between the two labellings.
    • Consider \[\alpha = \mu s, \;\; \beta = (1 - \mu) s\] where \(\mu \in (0, 1)\), \(s > 0\).
  • Interpretation:
    • \(\mu\): mean of the Beta
    • \(s\): measure of “peakiness” of the density, higher \(s\) corresponds to more peaked; roughly, \(s \approx\) number of data points that would make the posterior peaked like that.
  • Why we did this reparameterization?
    • \(\to\) it should now be more intuitive how we can use “side data” to inform \(\mu\)…

Second try (still suboptimal, but not as bad)

  • Estimate a failure probability \(\hat p_i\) for each type of rocket \(i\).
  • Fit a distribution \(p(\mu)\) on those \(\{\hat p_i\}\).
  • Use this distribution \(p(\mu)\) as the prior on \(\mu\)?
suppressPackageStartupMessages(require("ggplot2"))
suppressPackageStartupMessages(require("latex2exp"))

ggplot(df, aes(x = numberOfFailures / numberOfLaunches)) +
  geom_histogram() + 
  xlab(TeX("$\\hat{p}_i = \\textrm{numberOfFailures}_i / \\textrm{numberOfLaunches}_i$")) +
  geom_rug(alpha = 0.1) + 
  theme_minimal()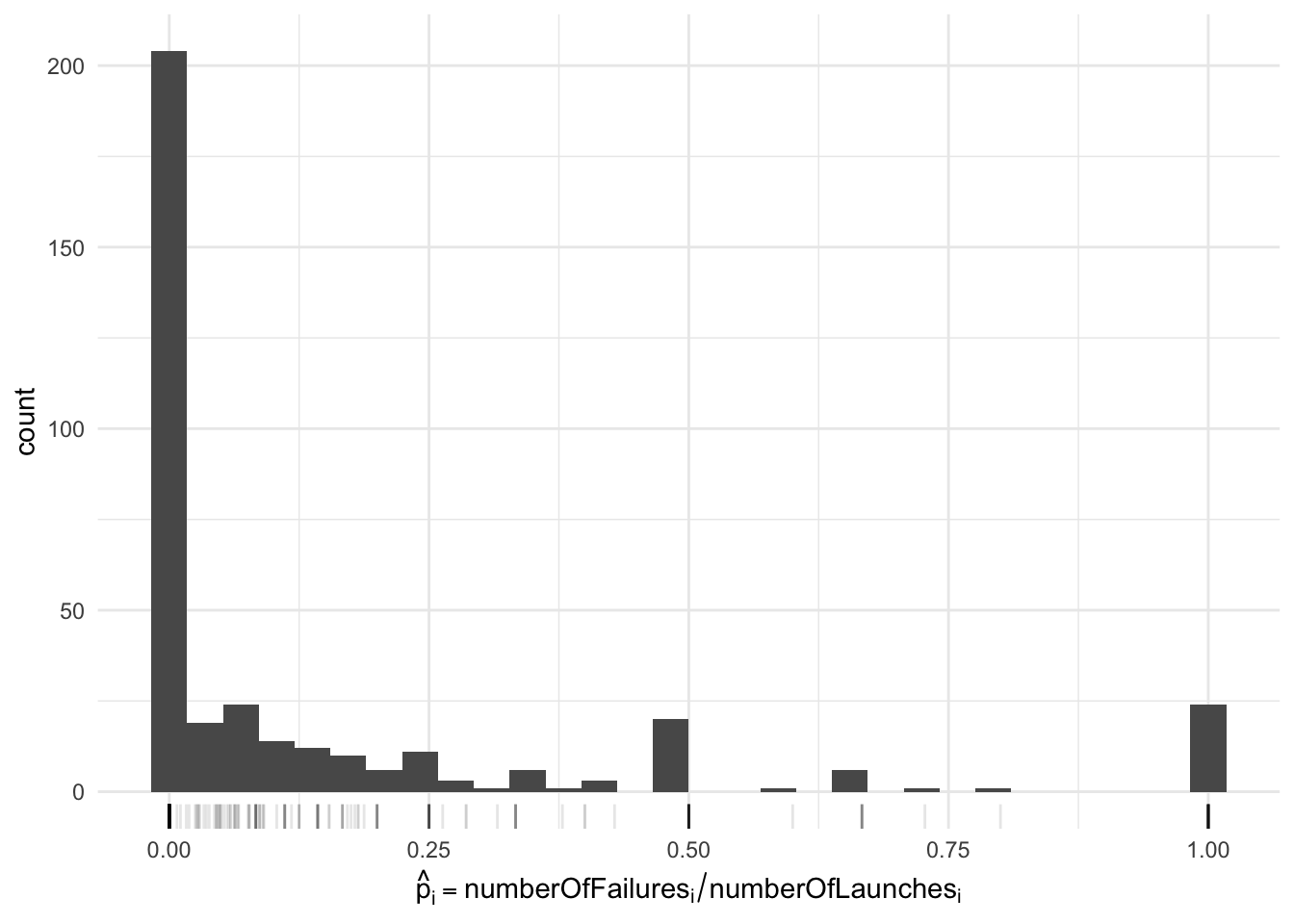

Question: what are the weaknesses of using a prior fitted on this histogram?

  • First, notice the “bumps” at 1/2 (and 1, 1/4, etc)…
    • Most of the counts at 1/2 correspond to types of rockets with 1 failure out of 2 launches!
    • But if you fit a curve to this data, these “bumps” will have a large undesirable effects.
    • More broadly, we want to take into account uncertainty in each of these \(\hat p_i\)’s.
  • Also: less clear how to generalize this method to handle the pseudo-sample-size \(s\).

Hierarchical models: a better way to use side data

Solution: go fully Bayesian!

Recall: our Bayesian recipe…

  1. Construct a probability model including
    • random variables for what we will measure/observe
    • random variables for the unknown quantities
      • those we are interested in (“parameters”, “predictions”)
      • others that just help us formulate the problem (“nuisance”, “random effects”).
  2. Compute the posterior distribution conditionally on the actual data at hand
  3. Use the posterior distribution to make a decision

What it means here: we model the launcher type’s population parameters (\(\mu, s\)) as random variables. We are not interested in these other launcher types, but they help us inform inference about the type of rocket we are interested in (i.e., “nuisance” parameters).

Graphical model

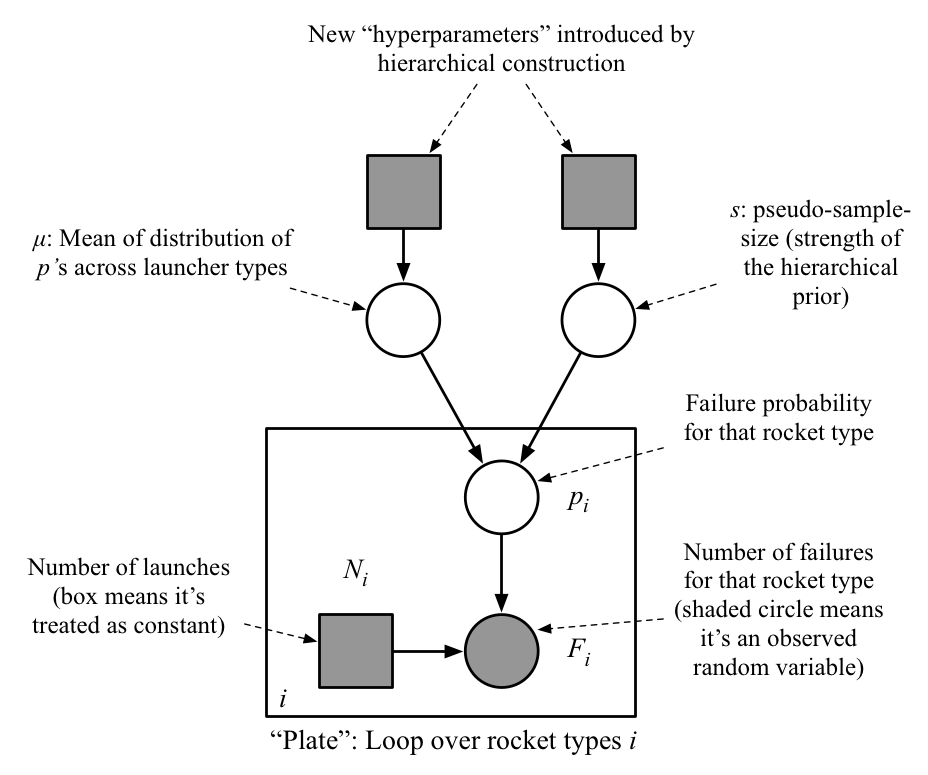
Mathematical description

  • Share these two “population parameters” across all launch types \[p_i | \mu, s \sim {\mathrm{Beta}}(\mu s, (1 - \mu) s)\]
  • Likelihood same as before: \(F_i | p_i \sim {\mathrm{Bern}}(n_i, p_i).\)
  • We still need to put prior on \(\mu\) and \(s\)…
    • …but as we’ll discuss next, you should expect this prior choice to be less sensitive.
    • Example: \(\mu \sim {\mathrm{Beta}}(1,1) = {\mathrm{Unif}}(0, 1)\), \(s \sim {\mathrm{Exp}}(1/10000)\)

PS: why we pick such a small value, \(1/10000\)?

  • Recall the parameter of an exponential is a rate which is 1/mean.
  • So a mean of 10000 encodes we put significant mass to values up to \(O(10000)\).
  • This is sometimes described as a “vague prior”.

Decrease prior choice sensitivity

It seems we have introduced new problems as now we again have hyper-parameters, namely those for the priors on \(\mu\) and \(s\)!

Key point: yes, but now we are less sensitive to these choices! Why?

Heuristic: look at the node \(n\) connected to the hyper-parameters…

  • If most of \(n\)’s edges link to hyper-parameters: posterior more sensitive to hyper-parameters.
  • If most of \(n\)’s edges link to random variables connected to data: posterior will probably be less sensitive.

Before going hierarchical: for maiden/early flights we had

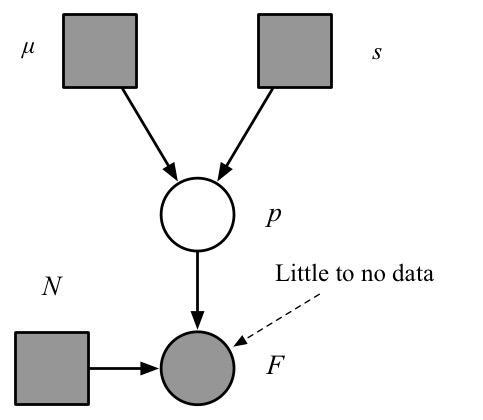
Note: \(p\) is connected to only a small number of observations.

After going hierarchical:

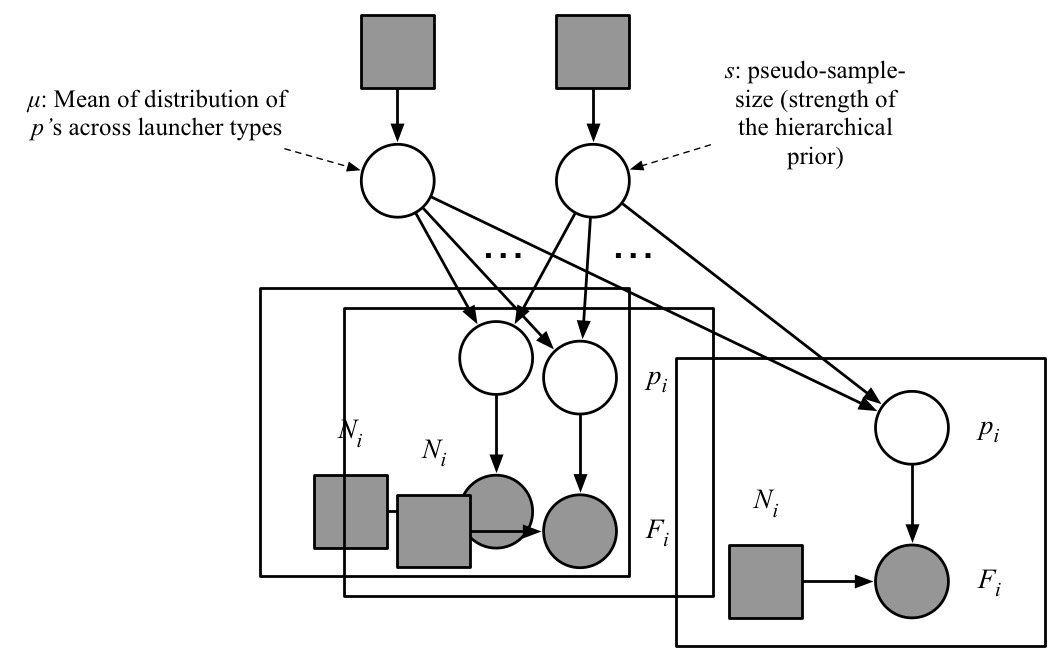
Note: \(\mu, s\) is connected to a large population of \(p_i\)’s, each linked with data.