Stan basics

Outline

Topics

  • Anatomy of a simple Stan program.
  • Interpreting the output of Stan.

Rationale

We will write many Stan models in the coming weeks, so we will cover here the key concepts needed to write in Stan. Similarities with simPPLe will help in this process.

Example

Review: code in simPPLe and analytic answer

Let us revisit the Doomsday model, which we wrote in simPPLe as follows:

source("../../solutions/simple.R")

doomsday_model <- function() {
  x = simulate(Unif(0, 5))
  observe(0.06, Unif(0, x))
  return(x)
}

posterior(doomsday_model, 100000)
[1] 1.103447

Recall the analytic answer that we computed in clicker questions was: \(\approx 1.117\).

Code in Stan

Today we will re-write this model in Stan instead of simPPLe. The main difference is that:

  • both simulate and observe will be denoted by ~in Stan,
  • to differentiate between observed and latent, Stan instead uses variable declarations (as data or parameters).

First, load rstan:

suppressPackageStartupMessages(require(rstan))

Then, as you did to test your install put the following code into a .stan file:

1data {
  real y; 
}

2parameters {
  real<lower=0, upper=5> x;
}

model {
3  x ~ uniform(0, 5);
4  y ~ uniform(0, x);
}
1
Variables introduced in a data block will be treated as observed.
2
Variables introduced in a parameters block will be treated as latent, i.e., unobserved.
3
Since x is declared latent (i.e., inside a parameters block), Stan will know to treat this as the counterpart of simPPLe’s x = simulate(Unif(0, 5)).
4
Since y is declared observed (i.e., inside a data block), Stan will know to treat this as the counterpart of simPPLe’s observe(0.06, Unif(0, x)).

Question: How does Stan gets the actual observed value \(y = 0.06\)?

Answer: When Stan gets called in R:1

fit = sampling(
  doomsday,         
1  data = list(y = 0.06),
  chains = 1,
2  iter = 100000
)
1
Pass in the values taken by the observed random variables.
2
The number of samples to compute (equivalent to \(M\) in our Monte Carlo notation) 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 4e-06 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.04 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:     1 / 100000 [  0%]  (Warmup)
Chain 1: Iteration: 10000 / 100000 [ 10%]  (Warmup)
Chain 1: Iteration: 20000 / 100000 [ 20%]  (Warmup)
Chain 1: Iteration: 30000 / 100000 [ 30%]  (Warmup)
Chain 1: Iteration: 40000 / 100000 [ 40%]  (Warmup)
Chain 1: Iteration: 50000 / 100000 [ 50%]  (Warmup)
Chain 1: Iteration: 50001 / 100000 [ 50%]  (Sampling)
Chain 1: Iteration: 60000 / 100000 [ 60%]  (Sampling)
Chain 1: Iteration: 70000 / 100000 [ 70%]  (Sampling)
Chain 1: Iteration: 80000 / 100000 [ 80%]  (Sampling)
Chain 1: Iteration: 90000 / 100000 [ 90%]  (Sampling)
Chain 1: Iteration: 100000 / 100000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.253 seconds (Warm-up)
Chain 1:                0.157 seconds (Sampling)
Chain 1:                0.41 seconds (Total)
Chain 1:

We can now compare the approximation provided by Stan:

fit
Inference for Stan model: anon_model.
1 chains, each with iter=1e+05; warmup=50000; thin=1; 
post-warmup draws per chain=50000, total post-warmup draws=50000.

      mean se_mean   sd  2.5%   25%   50%   75% 97.5% n_eff Rhat
x     1.12    0.01 1.25  0.07  0.19  0.55  1.68  4.45 10585    1
lp__ -0.37    0.01 0.63 -2.21 -0.41 -0.12 -0.04 -0.01  9987    1

Samples were drawn using NUTS(diag_e) at Tue Mar  5 11:45:15 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

Tips and tricks

Interpreting the output

  • Just as simple Monte Carlo and SNIS, the output of Stan/MCMC is a list of samples
  • In contrast to SNIS, the samples are equally weighted,
    • in other words, for MCMC we have \(W^{(m)}= 1/M\),
    • i.e., their structure is the same as samples from simple Monte Carlo!

To access the samples from a “fit” object when calling Stan, use:

samples = extract(fit)

head(samples$x)
[1] 0.7224132 3.7228678 2.2768091 1.0077302 4.9788992 0.6378141

As a sanity check, let’s make sure all the samples are greater than the observed lower bound of \(0.06\):

min(samples$x)
[1] 0.06000474

Question: denote the samples output from Stan by \(X^{(1)}, X^{(2)}, \dots, X^{(M)}\). What formula should you use to approximate \(\mathbb{E}[g(X) | Y = y]\) based on the Stan output?

  1. \(\sum_x p(x) g(x)\)
  2. \(\sum_x f(x) g(x)\)
  3. \(\frac{1}{M} \sum_{m=1}^M g(X^{(m)})\)
  4. \(\frac{1}{M} \sum_{m=1}^M f(X^{(m)}) g(X^{(m)})\)
  5. None of the above

As in simple Monte Carlo, use \(\frac{1}{M} \sum_{m=1}^M g(X^{(m)})\).

Plotting histograms

Since the samples are equally weighted, this makes it simpler to create plots, e.g., for a histogram:

hist(samples$x)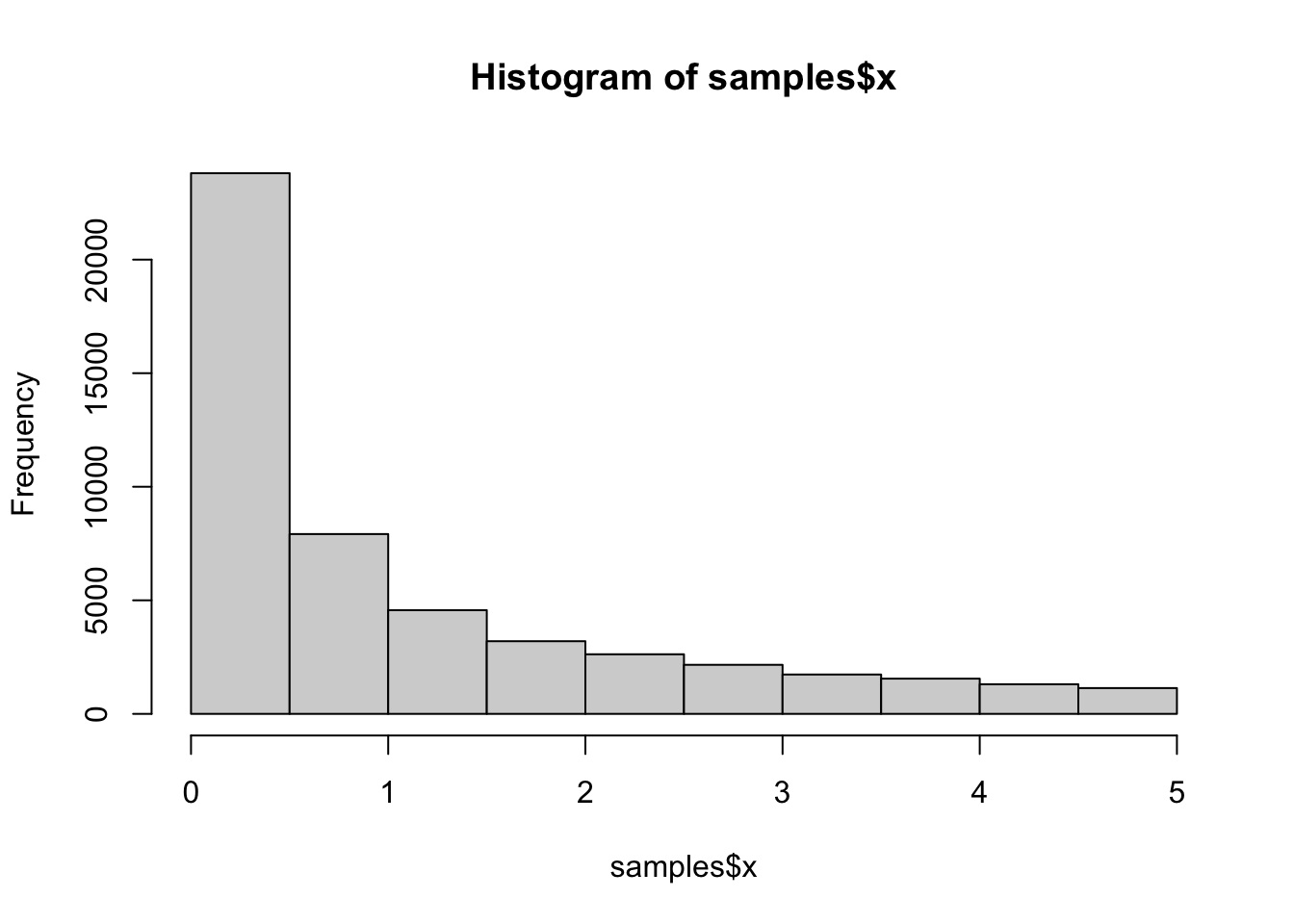

You can also use the bayesplot package which will be handy to create more complex plots from MCMC runs:

suppressPackageStartupMessages(require(bayesplot))
mcmc_hist(fit, pars = c("x"))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.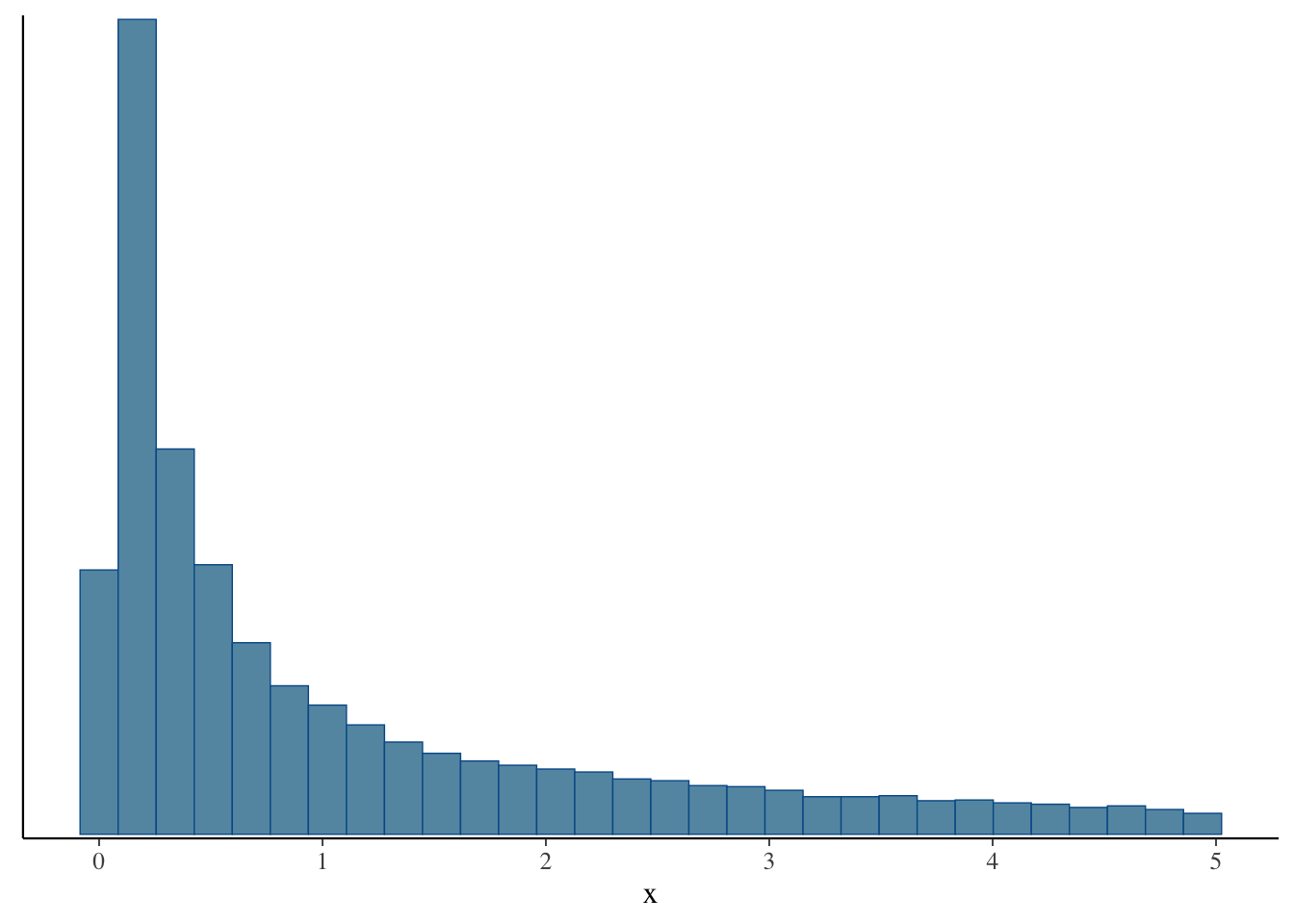

Footnotes

  1. when calling Stan from an R script, use stan(file = ...), but when calling Stan from R Markdown (as we do here), use sampling(name, ...), where the first argument, name matches the code block argument output.var = "name" (see the source of this page for an example).↩︎