Deterministic proposals

Outline

Topics

  • Deterministic proposals
  • Involutions
  • Proposal Jacobian determinants

Rationale

In our first exposure to MH, we defined the proposal as a probability distribution \(q(\cdot|x)\) based on the current point \(x\).

For HMC, it is more natural to consider the proposal as a deterministic function \(T(x)\).

We state a version of the MH algorithm based on such deterministic proposal here.

MH with deterministic proposals

Algorithm:

  1. Denote the current state by \(x \in \mathbb{R}^d\)
  2. Propose: \(x^* = T(x)\) for some deterministic proposal mapping \(T : \mathbb{R}^d \to \mathbb{R}^d\)
    • Assume that \(T\) satisfies \(T = T^{-1}\).
    • Terminology: \(T\) is an involution.
  3. Compute the ratio, \[r(x) = \frac{\gamma(x^*)}{\gamma(x)} | \nabla T(x) |,\] where \(| \nabla T(x) |\) denotes the Jacobian determinant.
  4. Accept \(x^*\) with probability \(\alpha(x) = \min(1, r(x))\), otherwise stay at \(x\).

Calculus review: do you remember what is the Jacobian determinant?

\[\begin{align*} \nabla T(x) &= \begin{bmatrix} \dfrac{\partial T_1}{\partial x_1} & \cdots & \dfrac{\partial T_1}{\partial x_n}\\ \vdots & \ddots & \vdots\\ \dfrac{\partial T_m}{\partial x_1} & \cdots & \dfrac{\partial T_m}{\partial x_n} \end{bmatrix} \\ |\nabla T(x)| &= |\det \nabla T(x)|. \end{align*}\]

Proposition: (Tierney, 1998) if \(T\) is a continuously differentiable involution, then the above algorithm is \(\pi\)-invariant.

Examples of involution

Swaps:

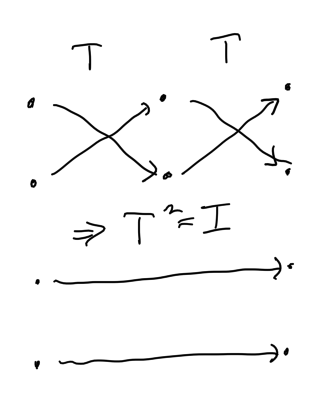
  • Set \(T(x_1, x_2) = (x_2, x_1)\).
  • To show involution, compute \(T^2(x) = T(T(x))\) and show \(T^2 = I\), the identity map.
  • \(T(T(x_1, x_2)) = T(x_2, x_1) = (x_1, x_2)\) ✅

Multiplicative proposal: complete the definition of \(T\) to make it an involution on \(\mathbb{R}\times \mathbb{R}^+\). \[T(x_1, x_2) = T(x, m) = (mx, \_\_).\]

  1. Any choice would work.
  2. \(T(x, m) = T(mx, m)\)
  3. \(T(x, m) = T(mx, m^2)\)
  4. \(T(x, m) = T(mx, 1/m)\)
  5. None of the above.

Correct answer is \(T(x, m) = T(mx, 1/m)\), since

\[\begin{align*} T(T(x, m)) &= T(mx, 1/m) \\ &= ((1/m)(mx), 1/(1/m)) \\ &= (x, m). \end{align*}\]

Question: Compute the Jacobian determinant of the multiplicative proposal involution.

You should get a triangular matrix i.e. in our context of the form

\[\begin{align*} \nabla T &= \begin{bmatrix} a_{11} & a_{12} \\ 0 & a_{22} \end{bmatrix}. \end{align*}\]

Now recall that from properties of triangular matrices, this means that to compute it determinant, you just have to compute the product of the diagonal entries, \(\det \nabla T = a_{11} a_{22}\).

  1. \(1/m\)
  2. \(1/m^2\)
  3. \(1/x\)
  4. \(1/x^2\)
  5. None of the above.

Correct answer is \(1/m\).

First, we compute the Jacobian matrix, where we denote \(T_1(x, m) = xm\) and \(T_2(x, m) = 1/m\):

\[\begin{align*} \nabla T(x, m) &= \begin{bmatrix} \dfrac{\partial T_1}{\partial x} & \dfrac{\partial T_1}{\partial m}\\ \dfrac{\partial T_2}{\partial x} & \dfrac{\partial T_2}{\partial m} \end{bmatrix} \\ &= \begin{bmatrix} m & x \\ 0 & -1/m^2 \end{bmatrix}. \end{align*}\]

Hence, the Jacobian determinant is \(|1/m|\). Since \(m \in \mathbb{R}^+\), \(|1/m| = 1/m\).

References

  • See Tierney, 1998 for the introduction of the notion of involutions and deterministic proposals to the MCMC literature.
  • See Green, 1995 for early use of the multivariate change of variable formula in MH acceptance ratios.