Practice questions (Quiz 2)

Caution

Page under construction: information on this page may change.

Outline

Topics

Representative example of questions to prep for Quiz 2.

Important note

Make sure to practice the similar page for Quiz 1 since quiz 2 will cover that material as well.

Libraries needed to run the example below

suppressPackageStartupMessages(require(rstan))

Model construction

Consider the following setup

You have a cohort of 15 unemployed persons who are all starting a job search process at the same time.
For each participant, you have collected 2 covariates: their age and their number of years of education.
You contact the participants each day for 10 days and record the day they secured a new job.
At the end of your study, 3 of the participants are still looking for a job.

Using the `~` notation

Define a Bayesian model to handle this dataset. Introduce all random variables, and specify for each its data type, if it observed or not.

Rao-blackwellization

Write the joint density of the model in the last part, before and after Rao-Blackwellization. You can introduce symbols for densities and CDFs, for example leave the density of the exponential as \(p_\text{Exp}(x; \lambda),\) and similarly use \(F_\text{Name}(\cdot; \cdot)\) to denote CDFs.

Model debugging

Let:

\(C(y)\) denote a 99% credible interval computed from data \(y\).
Let \(y\) and \(\check y\) denote a real and synthetic (simulated) data respectively.

Suppose you observed the following:

\(y_n \notin C(y_{\backslash n})\)
\(\check y_n \notin C(\check y_{\backslash n})\)
On both synthetic and real data, trace plots and ESS both look good.
You replicated these experiments several times and always get the same results.

What would you do next? Justify your answer.

Normalization constant

Consider the Bayesian model:

\[\begin{align*} X &\sim {\mathrm{Exp}}(1/100) \\ Y &\sim {\mathrm{Poisson}}(X). \end{align*}\]

When using MCMC, will the output change if, for \(x > 0\)…

You used \(\check f(x) = \exp(-(1/100) x)\) instead of \(f(x) = (1/100) \exp(-(1/100) x)\) for the prior?
You used \(\hat f(y|x) = x^y / y!\) instead of \(f(y|x) = \exp(-x) x^y / y!\) for the likelihood?

Intervals

Suppose you see the following output from a Stan MCMC fit object:

Inference for Stan model: anon_model.
1 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=1000.

            mean se_mean   sd  2.5%   25%   50%   75% 97.5% n_eff Rhat
slope       0.42    0.00 0.04  0.34  0.40  0.42  0.45  0.51   719    1
sigma       0.24    0.00 0.04  0.18  0.21  0.24  0.27  0.33   639    1
prediction  0.64    0.01 0.27  0.14  0.47  0.64  0.81  1.20  1023    1
lp__       21.32    0.06 1.04 18.46 20.94 21.62 22.09 22.36   331    1

Samples were drawn using NUTS(diag_e) at Thu Mar 14 14:41:50 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

Report a 80% confidence interval to capture the Monte Carlo error for the posterior mean of the prediction parameter.

Some of the following will be helpful in answering that question:

qnorm(0.8)

[1] 0.8416212

qnorm(0.9)

[1] 1.281552

qnorm(0.95)

[1] 1.644854

Report a 50% credible interval for the prediction parameter. You can ignore Monte Carlo error in this sub-question.

Bias and consistency

Let \(\hat G_M\) denote a Monte Carlo estimator based on \(M\) iterations, providing an approximation for an intractable expectation, \(g^* = \mathbb{E}_\pi[g(X)]\).

Define the notion of bias.
Define the notion of consistency.
In the context of Monte Carlo methods, what is more important, a bias of zero (unbiasness) or consistency? Why?

Stan-based prediction

Consider the code you wrote in Exercise 7 to perform Bayesian linear regression on galaxy distances and velocities:

data {
  int<lower=0> N; // number of observations
  vector[N] xs;   // independent variable
  vector[N] ys;   // dependent variable
}

parameters {
  real slope;
  real<lower=0> sigma;
}

model {
  // prior
  slope     ~ student_t(3, 0, 100);
  sigma     ~ exponential(0.001);

  // likelihood
  ys ~ normal(slope*xs, sigma);
}

How would you modify this code to predict the velocity of a galaxy at distance 1.5? Hint: use the function normal_rng(mean, sd) to generate a normal random variable with the provided mean and standard deviation parameters.

Metropolis-Hastings

Fill the two gaps in the pseudo code below:

Initialize \(X^{(0)}\) arbitrarily
For \(m = 1, 2, \dots, M\) do:
- Denote the proposal at iteration \(m \in \{1, 2, \dots, M\}\) by: \[\tilde X^{(m)}\sim q(\cdot | X^{(m-1)}).\]
- Compute the MH ratio: \[R^{(m)}= \frac{\gamma(\tilde X^{(m)})}{\gamma(X^{(m-1)})}.\]
- Sample an acceptance Bernoulli: \[A^{(m)}\sim \text{???}.\]
  - If \(A^{(m)}= 1\), we accept the proposed sample: \[X^{(m)}= \text{???}\]
  - Else, \(A^{(m)}= 0\), and we reject the proposed sample and stay at previous position: \[X^{(m)}= X^{(m-1)}.\]

Stan

Explain the difference between the parameters block and the transformed parameters block in Stan.
Why do you think Stan uses 4 independent chains by default?

Reasoning about MH

Consider the MH algorithm where we use as proposal a normal centered at the current point with standard deviation \(\sigma_p\).

You observe the following trace plot:

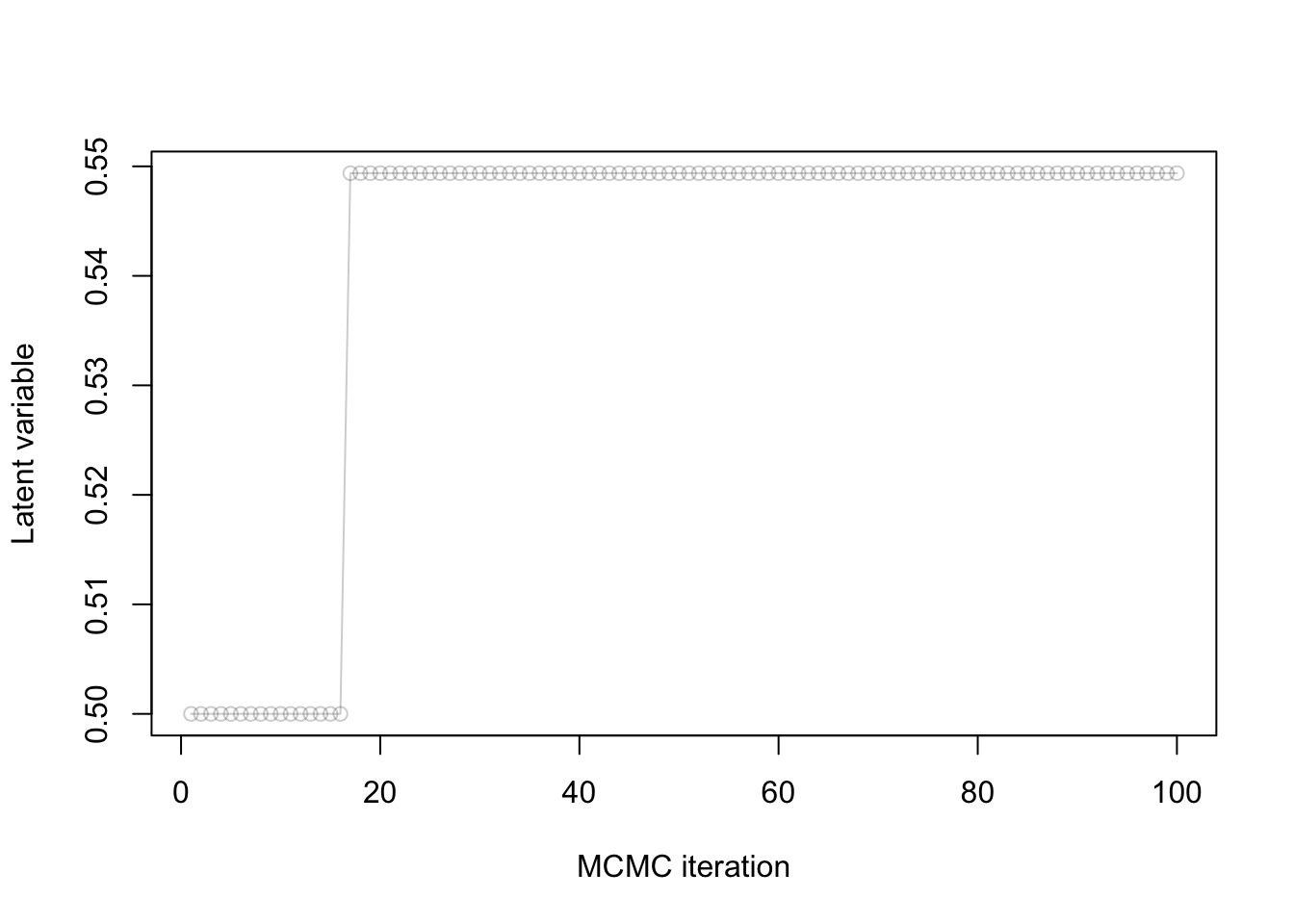
Is this chain mixing well?
Why or why not?
If it is not, what course of action do you recommend?

Irreducibility

Consider the following MH setup:

\(\gamma(x) = \mathbb{1}[x \in \{1, 2, \dots, 10\}]\)
\(q(x' | x) = \mathbb{1}[x' \in \{x-1, x+1\}]/2\).

Define irreducibility.
Prove that the MH algorithm is irreducible in this setup.

MCMC diagnostics

Explain how to detect slow mixing from a rank plot.

MCSE

How would you proceed if you want to decrease Monte Carlo Standard Error (MCSE)?

Debugging

You wish to write Stan model for logistic regression with normal priors on the parameters with prior variance 100.

Consider the following draft of a Stan model:

data { 
  int N
  array[N] int y
}

model {
  slope ~ normal(0, 100);
  intercept ~ normal(0, 100);
  for (i in 1:N) {
    y[i] ~ bernoulli(inv_logit(intercept + slope * i));
  }
}

Identify as many bugs as you can, and correct each.

Effective sample size from asymptotic variance

Recall that the CLT for i.i.d. and Markov chains give us the following approximations:

\(\sqrt{M} (\bar X_\text{Markov} - \mu) \approx \sigma_a G,\)
\(\sqrt{n_e} (\bar X_\text{iid} - \mu) \approx \sigma G,\)

where \(M\) is the number of iterations, \(n_e\) is the effective sample size, \(\bar X_\text{Markov}\) and \(\bar X_\text{iid}\) are the MC estimators based on MCMC and i.i.d. sampling respectively, \(G\) is standard normal, \(\mu\), \(\sigma\) are the posterior mean and standard deviation, and \(\sigma_a\) is the asymptotic variance.

Use these two approximations to write a formula for the effective sample size based on \(\sigma\), \(\sigma_a\) and \(M\).

Independence: prior vs posterior

Suppose we place a prior where \(X_1\) and \(X_2\) are independent, say \(X_i \sim {\mathrm{Bern}}(0.5)\) independently. If we condition on some data \(Y\), will \(X_1\) and \(X_2\) always be independent under the posterior?

Outline

Topics

Important note

Libraries needed to run the example below

Model construction

Using the ~ notation

Rao-blackwellization

Model debugging

Normalization constant

Intervals

Bias and consistency

Stan-based prediction

Metropolis-Hastings

Stan

Reasoning about MH

Irreducibility

MCMC diagnostics

MCSE

Debugging

Effective sample size from asymptotic variance

Independence: prior vs posterior

Using the `~` notation